From the given equation #r=theta-3*sin(theta+(5pi)/3)#
solve #r# when #theta=(2pi)/3#
#r=theta-3*sin(theta+(5pi)/3)#
#r=(2pi)/3-3*sin((2pi)/3+(5pi)/3)#
#color(red)(r=(2pi)/3-(3sqrt3)/2)#
Solve for the slope #m# with the formula
#color(blue)(m=(r' sin theta+r*cos theta)/(r' cos theta-r*sin theta)#
#r'=(dr)/(d theta)=1-3 cos (theta+(5pi)/3)#
#m=#
#(((1-3 cos (theta+(5pi)/3)) sin theta+(theta-3*sin(theta+(5pi)/3))*cos theta))/(((1-3 cos (theta+(5pi)/3) )*cos theta-(theta-3*sin(theta+(5pi)/3))*sin theta)#
with the value #theta=(2pi)/3#
#m=#
#(((1-3 cos ((2pi)/3+(5pi)/3)) sin ((2pi)/3)+((2pi)/3-3*sin((2pi)/3+(5pi)/3))*cos ((2pi)/3)))/(((1-3 cos ((2pi)/3+(5pi)/3) )*cos ((2pi)/3)-((2pi)/3-3*sin((2pi)/3+(5pi)/3))*sin ((2pi)/3))#
#m=#
#(((1-3 cos ((7pi)/3)) sin ((2pi)/3)+((2pi)/3-3*sin((7pi)/3))*cos ((2pi)/3)))/(((1-3 cos ((7pi)/3) )*cos ((2pi)/3)-((2pi)/3-3*sin((7pi)/3))*sin ((2pi)/3))#
#m=((1-3/2) (sqrt3/2)+((2pi)/3-(3sqrt3)/2)(-1/2))/((1-3/2 )*(-1/2)-((2pi)/3-(3*sqrt3)/2)((sqrt3)/2)#
#m=(3sqrt3-2pi)/(15-2pisqrt3)#
convert #(r, theta)# to #(x, y)#
#x_1=r cos theta=((2pi)/3-(3sqrt3)/2)cos ((2pi)/3)=(3sqrt3)/4-pi/3#
#x_1=(3sqrt3)/4-pi/3#
#y_1=r sin theta=((2pi)/3-(3sqrt3)/2)sin ((2pi)/3)=(sqrt3*pi)/3-9/4#
#y_1=(sqrt3*pi)/3-9/4#
Solve the tangent line using #m# and #(x_1, y_1)#
#y-y_1=m(x-x_1)#
#y-(sqrt3*pi)/3+9/4=((3sqrt3-2pi)/(15-2pisqrt3))(x-(3sqrt3)/4+pi/3)#
Kindly see the graph of #r=theta-3*sin(theta+(5pi)/3)# and tangent line #y-(sqrt3*pi)/3+9/4=((3sqrt3-2pi)/(15-2pisqrt3))(x-(3sqrt3)/4+pi/3)#
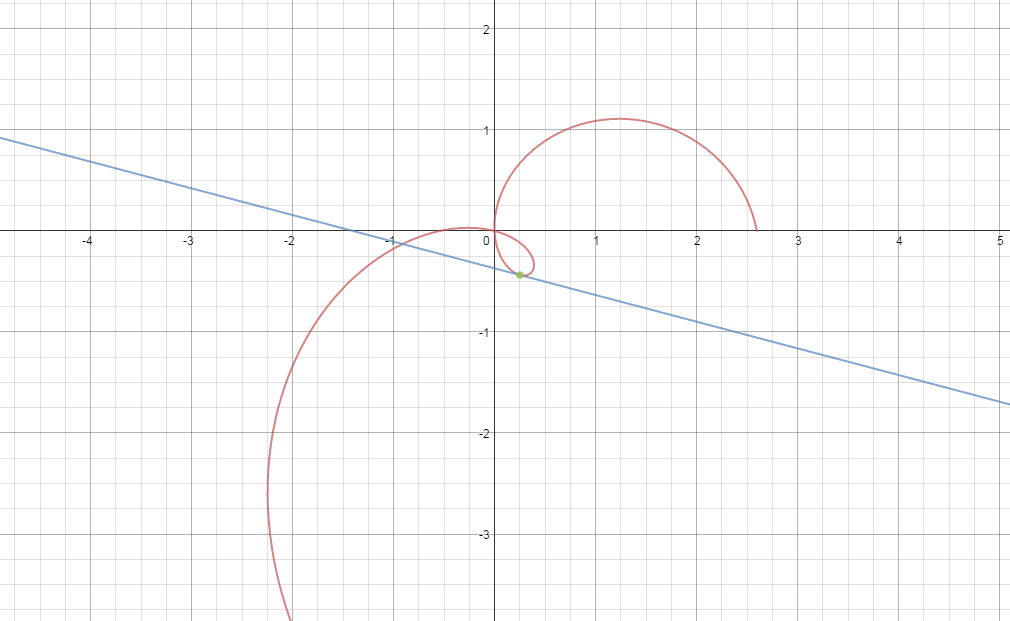
God bless...I hope the explanation is useful.

