A Ferris wheel 50ft in diameter makes one revolution every 40sec. If the center of the wheel is 30ft above the ground, how long after reaching the low point is a rider 50ft above the ground?
1 Answer
Jun 8, 2016
I found:
Explanation:
Consider the (confused) diagram:
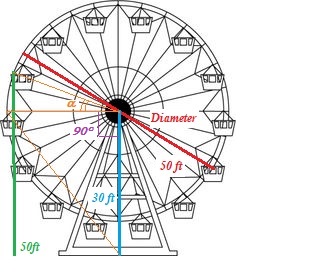
We can evaluate the angle
so:
So
Now:
Angular velocity is
To describe

