A parallelogram has sides with lengths of 9 and 8 . If the parallelogram's area is 32 , what is the length of its longest diagonal?
1 Answer
Jun 20, 2016
It is
Explanation:
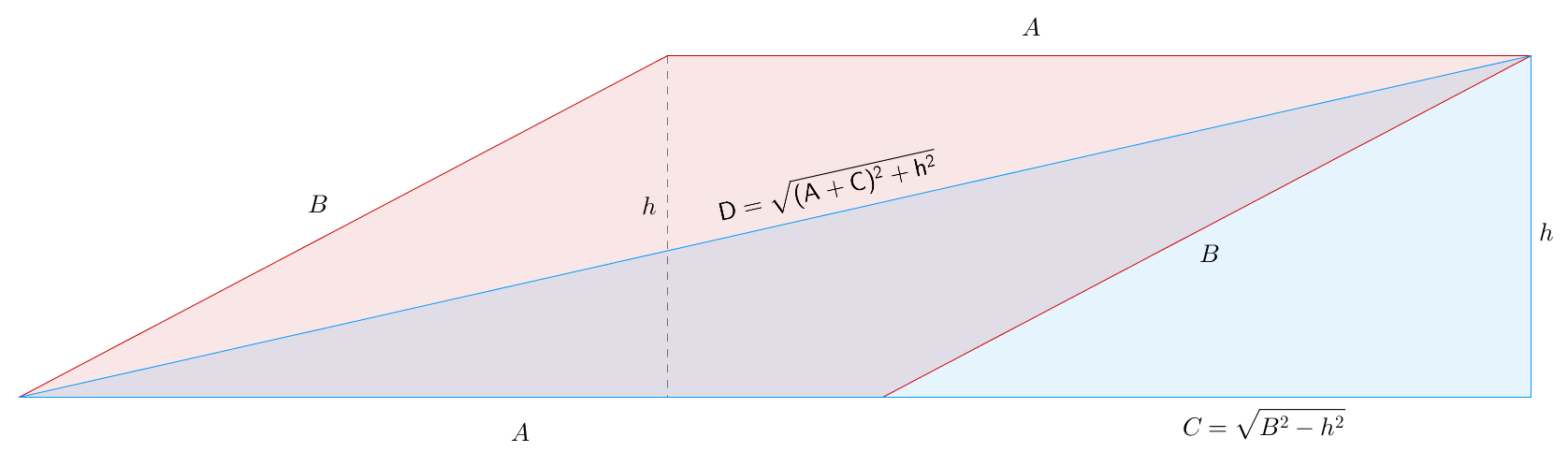 made with GeoGebra
made with GeoGebra
Consider the image. From the initial data we have
We know that the area is
For the longest diagonal we need to know
Finally, the diagonal is

