Question

For the reaction `X + Y -> Z`, the following data was obtained. Answer the following questions? Is there any missing info I need to do this?? What is the best way to learn kinetics?

For the reaction `X + Y -> Z`, the following data was obtained:

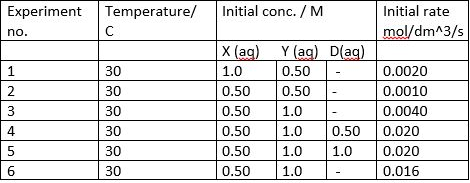
Answer the following questions:

1. Write a general rate law for the reaction.
2. Find the order with respect to each reactant.
3. Find the new rate if the concentration of `Y` was doubled and the old rate was `"0.004 mol/dm"^3cdot"s"`?
4. Describe the role of `D` in the reaction.
5. Draw a reaction-coordinate diagram for the reaction in the presence of `D` and in the absence of `D`.
6. Compare trials 3 and 6, and explain how the rate in trial 6 is fater, but the concentrations are the same.

Answer 1

As an overall observation, there is no data missing from the table---it's on purpose. All the information you need is in the question information.

And the best way to learn kinetics is to have an answer key and to try practice problems. It's not easy, so you'll need to put in the practice.

Some general tips:

• Make sure you know the difference between the rate law for the reaction, the rate of reaction `r(t)`, the rate constant `k`, and the rate of disappearance of reactant `-(d[R])/(dt)` or rate of appearance of product `(d[P])/(dt)`. These can often feel similar but they're not the same.
• When determining reaction order, don't be afraid to make up numbers and seeing what happens to `r(t)` when you keep one initial concentration constant and change the other one.

The point is to see relationships between changes in rate and changes in reactant concentration.

• Make sure you know how to write a rate law inside and out; it's often a useful equation to know how to work with, and is central to essentially any kinetics problem.

---

DISCLAIMER: LONG ANSWER!

(1) WRITING A RATE LAW

The rate law for the reaction is in general written as:

`\mathbf(r(t) = k[X]^m[Y]^n)`

`= \mathbf(-1/(nu_X)(d[X])/(dt) = -1/(nu_Y)(d[Y])/(dt) = 1/(nu_Z)(d[Z])/(dt))`

for the reaction

`nu_X X + nu_Y Y -> nu_Z Z`

where:

• `r(t)` is the rate as a function of time.
• `nu` is the stoichiometric coefficient.
• `k` is the rate constant, in units of `1/("M"^(-1 + m + n)cdot"s")` and `"1 M" = "1 mol/dm"^3`.
• `pm(d["compound"])/(dt)` is the rate of disappearance of reactant (negative) or appearance of product (positive).
• `m` and `n` are the orders of each reactant---having no relevance to the stoichiometry of the reaction at all.

For this, `nu_X = nu_Y = nu_Z = 1`, and we need to find `m` and `n`. We don't really need `k`, apparently.

(2) FINDING THE ORDERS OF EACH REACTANT

For the reaction

`"X"(aq) + "Y"(aq) -> "Z"(aq),`

we are basically looking at what happens when we change the initial concentrations of each reactant while keeping the other constant.

We're "rigging" the reaction to see what the orders (contributions) of each reactant are with respect to the rate.

The order for each reactant is found like so:

1. Look at two trials, where one reactant's initial concentration is kept the same for both trials.
2. Now look at the other reactant. What happened to its initial concentration?
3. Now inspect the rate in `"mol/dm"^3cdot"s"`. What happened to the rate?
4. Based on that, you should be able to find the order.

For trials 1 and 2, halving `[X]` halved the rate. Looking back at the rate law, basically, we are saying:

`[X]^m -> (([X])/2)^m` with `[Y]^n -> [Y]^n` causes `r(t) -> (r(t))/2`.

Therefore `m = 1`; that is, the order of `X` is `color(blue)(1)`.

For trials 2 and 3, doubling `[Y]` quadrupled `r(t)`. Basically, we are saying:

`[Y]^n -> (2[Y])^n` with `[X]^m -> [X]^m` causes `r(t) -> 4r(t)`.

So, `n = 2`, because `2^2 = 4`; that is, the order of `Y` is `color(blue)(2)`.

(3) FINDING A NEW RATE BASED ON NEW CONCENTRATIONS

We already got the information we needed for this in part 2.

Since we know the order of `Y` is `2`, compare to trial 3; we doubled `[Y]`, so the rate quadruples, just like going from trial 2 to 3.

Therefore, without doing much work, `color(blue)(r(t) = "0.016 mol/dm"^3cdot"s")`.

(4) ROLE OF D

Considering trials 4 and 5, the only trials to use `D`, the rate multiplied by `5`, for both of those two concentrations of `D`, relative to trial 3.

That tells me it's a catalyst, because a catalyst changes the mechanism of the reaction in some way, making it faster.

A common way it does so is by lowering the activation energy.

But it's surprising that the rate was the same for trials 4 and 5. I guess it means...

• some excess `D` was not used, OR
• the limit to the catalyst's activity was reached.

(5) REACTION COORDINATE DIAGRAMS

For this, that is asking you to use your answer in part 4 to draw a reaction coordinate diagram in the presence and absence of `D`. Recall that it is basically a plot of energy vs. the progress of the reaction.

As I said earlier, the activation energy, `E_a` is lower, and additionally, the mechanism is probably different.

For this diagram, `E_a` is the activation energy without `D`, and `E_a^"*"` is with `D`. The dip in the curve is an intermediate formed as a result of using `D`, and we don't need to know what it actually is.

I made up the curve, but it illustrates the idea: `\mathbf(E_a)` is lowered by `D`, the catalyst, speeding up the rate of reaction.

The products are lower in energy, indicating an energetically favorable reaction. That's an assumption, which is just saying that the reaction should happen.

(6) COMPARING TRIALS 3 AND 6

As for trial 6, we know that in comparison to trial 3, the reaction conditions are pretty much the same, except no `D` was added for trial 6. My concern is that it's not completely true.

Everything looks similar, but remember, trials 4 and 5 had to have happened right before trial 6.

So, I would expect that some catalyst `D` was not fully removed from solution.

That should make sense because `D` is aqueous, so it must have been soluble, and soluble catalysts are harder to remove than insoluble catalysts. You can just scoop out a solid catalyst. You can't just do that for a dissolved catalyst!

So, probably, some residual `D` is still there, and the reaction is still faster than it would be without `D`, but not as fast as it would be with more `D`.