Question

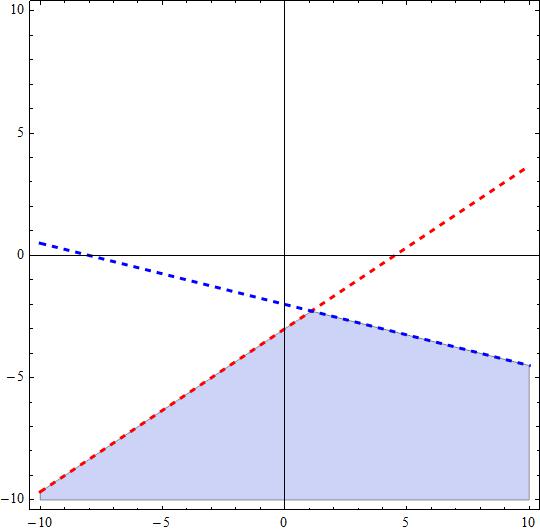
How do you graph the inequality `2x - 3y>9` and `- x - 4y> 8`?

Answer 1

Solution set of a system of 2 linear function

Explanation:

Bring the 2 inequalities to standard form:
2x - 3y - 9 > 0 (1)
-x - 4y - 8 > 0 (2).
First graph the 2 lines
Graph Line y1 = 2x - 3y - 9 = 0 by its 2 intercepts.
Make x = 0 --> y = -3.
Make y = 0 --> `x = 9/2`
the solution set of inequality (1) is the area above the Line y1.
Graph Line y2 = -x - 4y - 8 = 0 by its 2 intercepts.
Make x = 0 --> y = -2
Make y = 0 --> x = -8
To find the solution set, check the position of the origin (0, 0).
Replace x = 0 and y = 0 into the inequality (1), we get -9 > 0. That is not true. Consequently, the solution set of inequality (1) is the area below the Line y1.
Replace x = 0 and y = 0 into inequality (2) --> -8 > 0. Not true. Then, the solution set is the area below the Line 2.
The solution set of the system is the commonly shared area.
graph{2x - 3y - 9 = 0 [-10, 10, -5, 5]}
graph{-x -4y - 8 = 0 [-10, 10, -5, 5]}

Answer 2

See below

Explanation:

Given the inequalities, plot them as equalities, resulting two lines.

Determine the semi-plane which obeys the inequality. This is done easily at the `y` intersections.

For the first inequality we have

`2 cdot 0 -3 y > 9` so the feasible region at that point is

`y < -3`

For the second inequality we have

`-0-4y>8` so the feasible region at that point is

`y < -2`

The feasible region, in the attached figure, satisfying both inequalities, appears in light blue.

A short notation for this region is

`min(2 x - 3 y - 9 , -x - 4 y - 8)> 0`