Question

A parallelogram has sides A, B, C, and D. Sides A and B have a length of `5` and sides C and D have a length of `8`. If the angle between sides A and C is `(5 pi)/8`, what is the area of the parallelogram?

Answer 1

`"Total Area" ~~ 36.96`

Explanation:

So let's sketch the scenario. Remember that in a parallelogram, opposite angles are congruent and adjacent angles are supplementary.

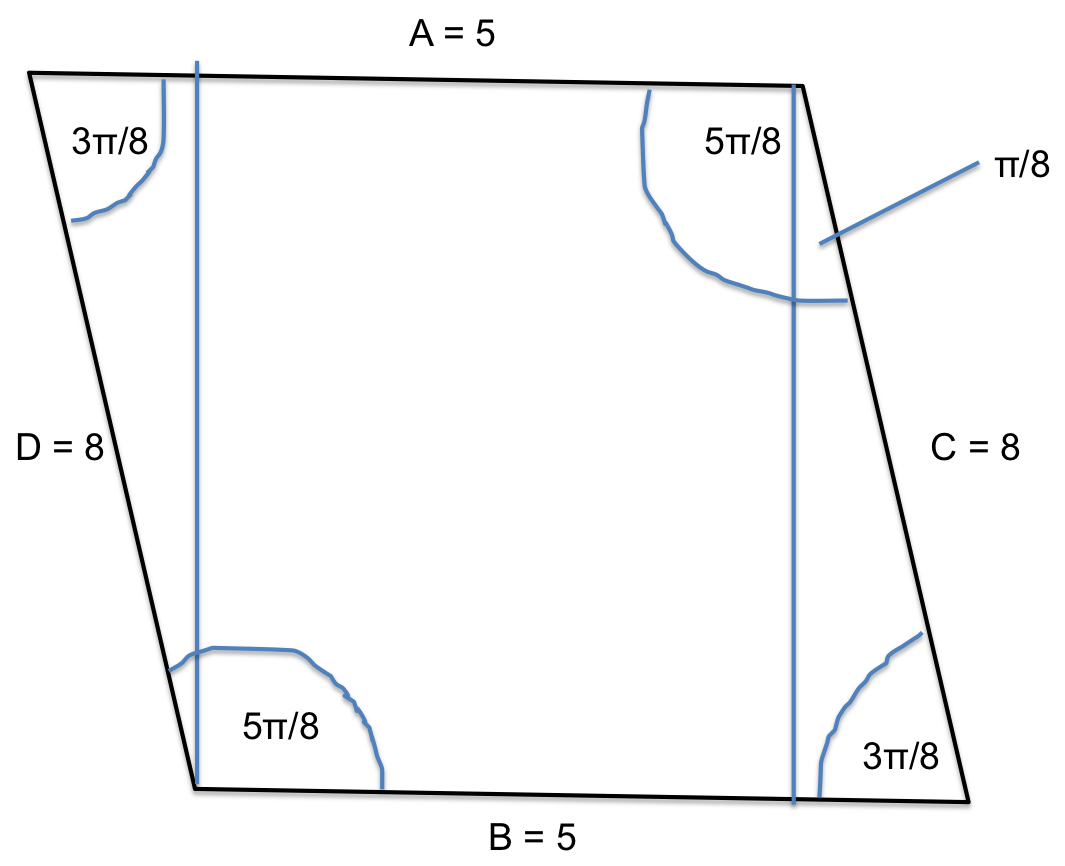
To find the area, we will split the shape into three shapes. Two right angled triangles and a rectangle.

We find the length of the vertical lines (the height of the triangles) by trigonometry. Remember SOH CAH TOA, so sine is opposite/hypotenuse.

`sin((3pi)/(8)) = y/8`

`y = 8sin((3pi)/8) ~~ 7.39` but we'll keep it in it's exact form for now.

We find the base of the triangles with the same technique:

`sin(pi/8) = x/8`

`x = 8sin(pi/8) ~~ 3.06`

The area of each triangle is given by

`A_("triangle") = 1/2a*b*sin(C)`

If we use `a and b` to be the base and height this reduces to

`A_("triangle") = 1/2xy = 32sin((3pi)/8)sin(pi/8)`

The area outside the rectangle is given by `2A_("triangle") ~~ 22.63`.

The rectangle's dimensions are given by the height of the triangles and `5- "the base of the triangles"`

`A_("rectangle") = y(5-x) = 8sin((3pi)/8)*(5-8sin(pi/8)) ~~ 14.33`

`"Total Area" = A_("rectangle") + 2A_("triangle")`

`"Total Area" ~~ 36.96`

As a sense check, if the shape was just a rectangle the area would be 40 so this is in the right neck of the woods at least.