How do you find the axis of symmetry, graph and find the maximum or minimum value of the function y = 2x^2 - 4x -3?
1 Answer
Axis of symmetry
Minimum value of the function
See the explanation for the graph
Explanation:
The solution:
To find the Axis of symmetry you need to solve for the Vertex
Formula for the vertex:
From the given
Axis of symmetry:
Since
Minimum value
The graph of
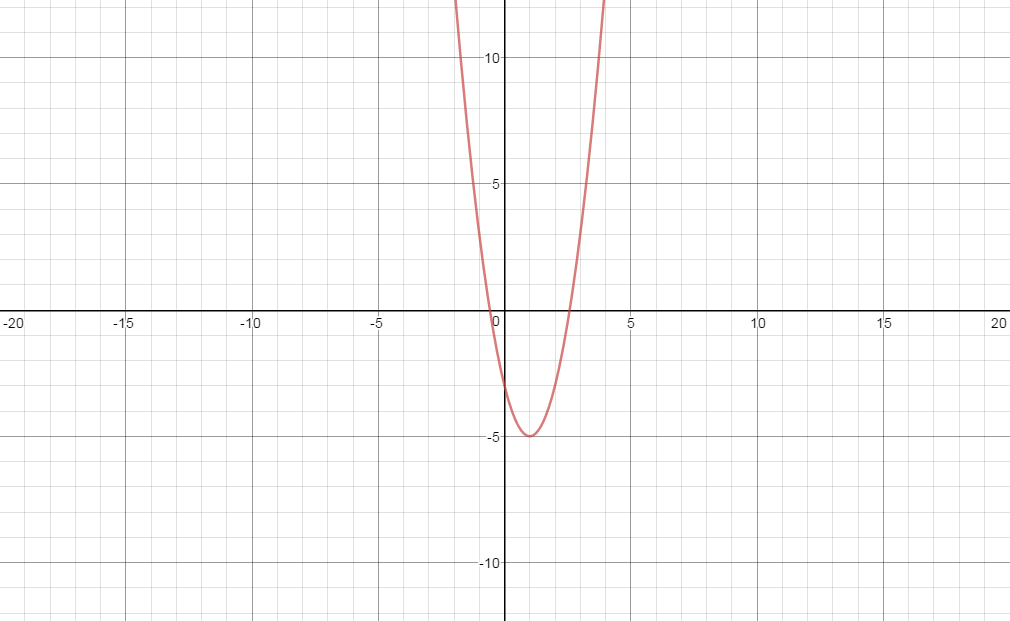 Desmos.com
Desmos.com
To draw the graph of
When
and when
We have two points at
God bless...I hope the explanation is useful.
