Question

How do you find the exact value of `sin(0)`?

Answer 1

`sin0˚ = 0`

Explanation:

By the unit circle:

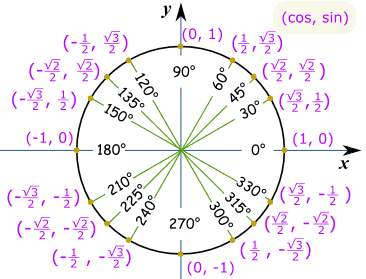
As you can see, pairs are ordered in the manner of `(cos,sin)`. In other words, the `x` value is `cos` and the `y` value is `sin`.

Since in this problem we're dealing with the sine function, you can ask yourself: What is the y-value at `0˚`?

Well, the point at `0˚` is `(1, 0)`, and the `y` value here is 0. The hypotenuse, although measuring `1` unit, doesn't matter, because `0/a, a != 0`, always equals `0`, no matter the value of `a`. Hence, `sin0˚ = 0`.

Practice exercises:

`1.` Find the values of the variables in the following blank unit circle.

`2.` Determine the following exact values:

a) `sin240˚`

b) `cos(pi/2)`

c) `tan((7pi)/6)`

Hopefully this helps, and good luck!