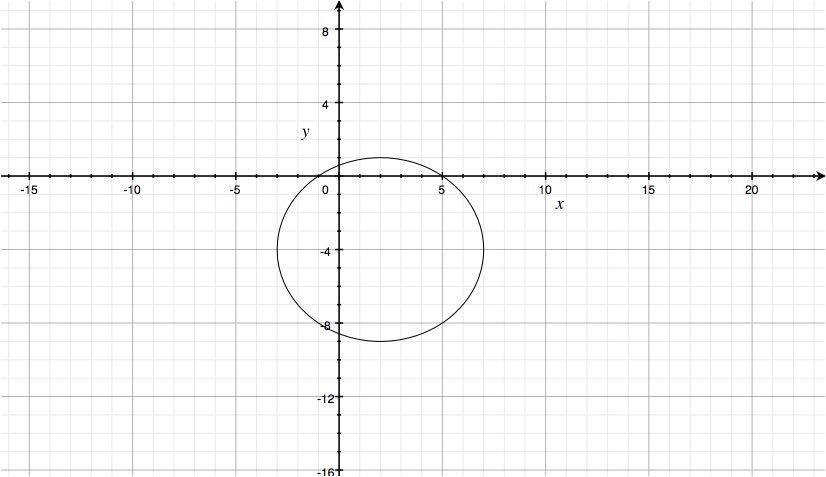
How do you find the center and radius of the circle #x^2+y^2-4x+8y-5=0 #?

Question

7972 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-25T02:05:50

Radius: #5# units
Center: #(2, -4)#

Do a double completion of square; the x's with the x's and the y's with the y's.

#1(x^2 - 4x + m - m) + 1(y^2 + 8y + n - n) - 5 = 0#

#m = (b/2)^2" AND " n = (b/2)^2#

#m = (-4/2)^2" AND "n = (8/2)^2#

#m = 4" AND "n = 16#

#1(x^2 - 4x + 4 - 4) + 1(y^2 + 8y + 16 - 16) = 0 + 5#

#1(x^2 - 4x + 4) - 4 + 1(y^2 + 8y + 16) - 16 = 5#

#(x - 2)^2 - 4 + (y + 4)^2 - 16 = 5#

#(x - 2)^2 + (y + 4)^2 = 5 + 16 + 4#

#(x - 2)^2 + (y + 4)^2 = 25#

In the form #(x - a)^2 + (y - b)^2 = r^2#, the radius is given by #r# and the centre #(a, b)#.

Hence, the centre is at #(2, -4)# and the radius measures #5# units. The graph of this circle confirms.

grapher (my computer)

Hopefully this helps!