Question

The surface tension of benzene at 20°C is 28.85 dyne/cm. In a capillary apparatus the liquid rose to a height of 1.832 cm. The density of benzene is 0.8765 g/mL. How would you calculate the diameter of the capillary tube in mm?

Answer 1

The diameter of the capillary tube is 0.366 mm.

Explanation:

One method for measuring the surface tension of a liquid is to measure the height the liquid rises in a capillary tube.

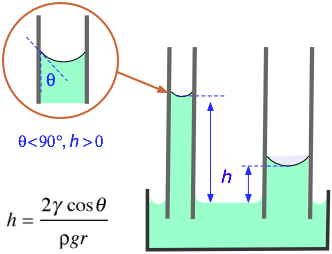
The formula is

`color(blue)(|bar(ul(color(white)(a/a) h = "2γcosθ"/"ρgr" color(white)(a/a)|)))" "`

where

`h` = the height the liquid rises in the capillary
`γ` = the surface tension
`θ` = the angle of contact with the surface
`ρ` = the density of the liquid
`g` = the acceleration due to gravity
`r` = the radius of the capillary

We can rearrange the equation to get

`color(blue)(|bar(ul(color(white)(a/a) r = "2γcosθ"/(hgρ)color(white)(a/a)|)))" "`

For most liquids and clean glass, the contact angle `θ` is nearly zero.

If `θ ≈ 0`, then `cosθ ≈ 1`, and the equation reduces to

`color(blue)(|bar(ul(color(white)(a/a) r = "2γ"/(hgρ)color(white)(a/a)|)))" "`

In your problem,

`γ = "28.85 dyne/cm"`
`h = "1.832 cm"`
`ρ = "0.8765 g/mL " = "0.8765 g/cm"^3`
`g = "981 cm·s"^"-2"`

`r = (2 × 28.85 color(red)(cancel(color(black)("dyne·cm"^"-1"))))/(1.832 color(red)(cancel(color(black)("cm"))) × 981 color(red)(cancel(color(black)("cm·s"^"-2"))) × 0.8765 color(red)(cancel(color(black)("g·cm"^"-3")))) × (1 color(red)(cancel(color(black)("g")))·"cm"·color(red)(cancel(color(black)("s"^"-2"))))/(1 color(red)(cancel(color(black)("dyne")))) = "0.0366 cm" = "0.366 mm"`