How do you find the angles of a triangle given side a = 10, side b = 10, base = 15?
1 Answer
Sep 17, 2016
see below.
Explanation:
Given is that 2 sides are of same length i.e. 10cm. This tells us that this is an isosceles triangle.
{ Isosceles triangles have 2 same angles and one different angle .}
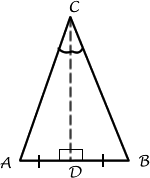
so using above picture let AC and BC be 10cm. And AB be 15 cm.
Now find CD using Pythagoras theorem, {then later the angle will be found}
Now apply trigonometric ratio(s)
Hence
Therefore
Now its simple,
hence

