Draw a random line segment and then trisect it?
2 Answers
See below.
Explanation:
In one extremity of the random line segment, along a line slanted and passing by this extremity, draw three equal length segments. Then, using the Thales of Miletus theorem,
https://en.wikipedia.org/wiki/Thales
you can divide the random segment into three equal subsegments.
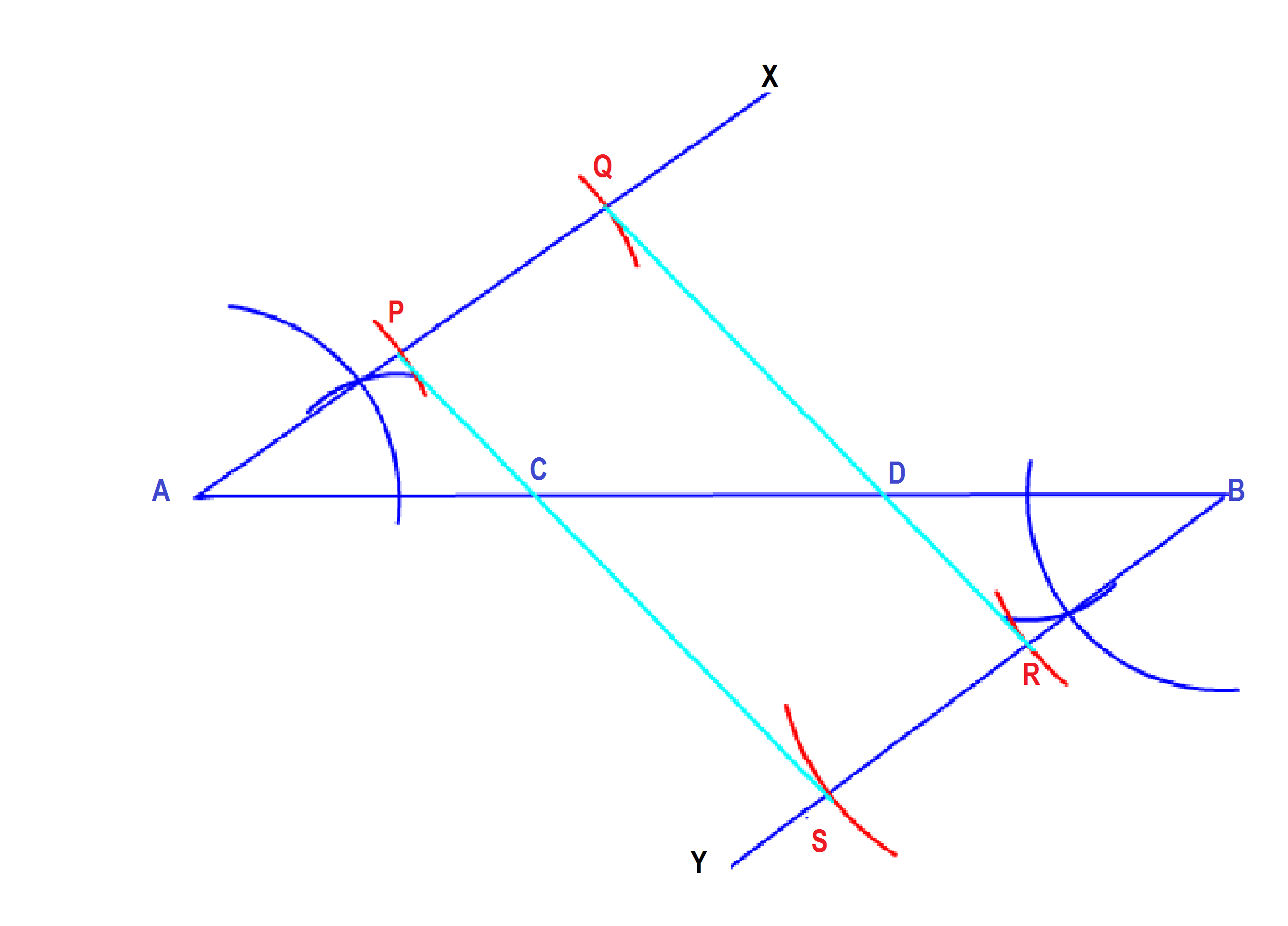
STEPS FOLLOWED
-
A random line segment is first drawn by a ruler and a pencil.
-
Two equal alternate interior angles
#/_XAB and /_YBA# of suitable measure are drawn at A and B respectively with the help of a ruler and a pencil compass . -
Two line segments
#(AP and PQ)# of same suitable length are cut off from AB by a pencil compass. -
Another two line segments
#(BR and RS)# of same suitable length as#AP and PQ# are also cut off from AB by a pencil compass. -
Finally
#P,S and Q,R# are joined with the help of a ruler and a
pencil.
As a result the line segment AB is trisected at C and D. The equality of length of three line segments AC,CD and DB is verified with the help of a divider.


