A parallelogram has sides with lengths of #15 # and #8 #. If the parallelogram's area is #8 #, what is the length of its longest diagonal?
1 Answer
Sep 28, 2016
Longest Diagonal:
Explanation:
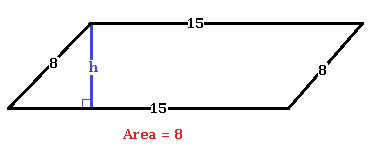
The height of the parallelogram,
Extending the side with length
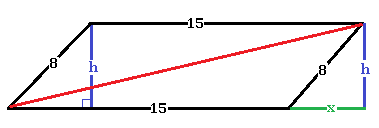
Applying the Pythagorean Theorem:
We can see that the length of the extension,
And the longest diagonal of the original parallelogram is
