How come #4y + 2x^2 = 20# and #x^2 +y = -9# are not linear functions?
2 Answers
A linear function can be of the following forms:
•
•
•
As I'm sure you've noticed, these forms all have a degree of
The two relations you are given do not have a degree of
If you are given a graph with a relation drawn on it, and asked to identify whether or not it's a linear relation, all you have to do is see if the graph is in a straight line. If it isn't, then it isn't a linear relation. If it is, it is a linear relation.
Finally, to prove that the given equations aren't linear relations:
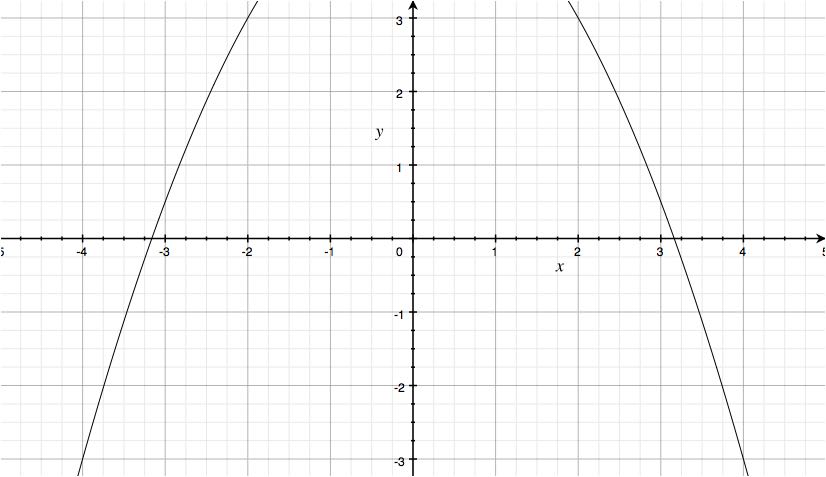
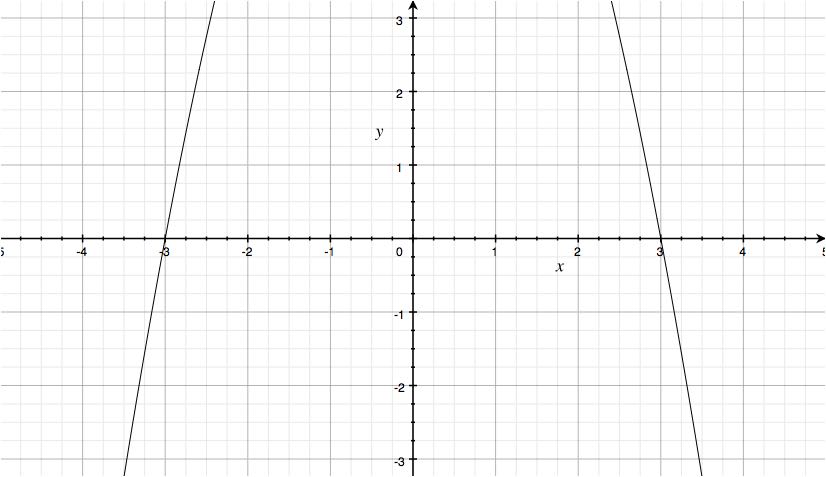
Hopefully this helps!
Linear functions properties
#color(blue)("Their graphs are straight lines"#
#color(blue)("Linear functions are in the form"# #color(blue)(f(x)=ax+b#
#"Where"# #x# #"is the variable"#
#color(blue)("There is only one variable"#
#color(blue)("The highest power of the variable is 1"#
Now we can check whether these equations are linear equations
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(red)(4y+2x^2=20#
graph{4y+2x^2=20}
This is not a linear equation as you can see
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(red)(x^2+y=-9#
graph{x^2+y=-9}
This is not a linear equation as you can see
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So,these are not linear functions


