Question

How come `4y + 2x^2 = 20` and `x^2 +y = -9` are not linear functions?

Answer 1

A linear function can be of the following forms:

•`y = mx + b`
•`y - y_1 = m(x - x_1)`
•`Ax + By - C = 0`

As I'm sure you've noticed, these forms all have a degree of `1`. The degree of a function is the highest exponent of any variable in an expression or function. For example, the degree in `y = 4x^3 + 2x` is `3` since the highest exponent is `3`.

The two relations you are given do not have a degree of `1`.

If you are given a graph with a relation drawn on it, and asked to identify whether or not it's a linear relation, all you have to do is see if the graph is in a straight line. If it isn't, then it isn't a linear relation. If it is, it is a linear relation.

Finally, to prove that the given equations aren't linear relations:

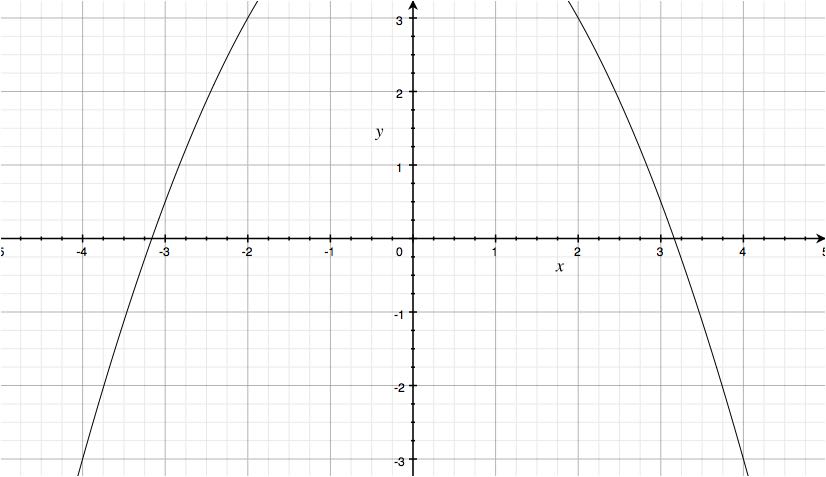
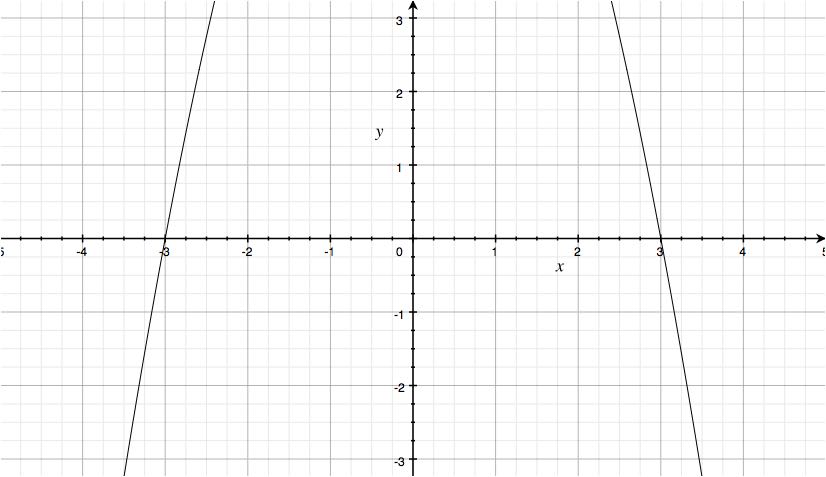
Hopefully this helps!

Answer 2

Linear functions properties

`color(blue)("Their graphs are straight lines"`

`color(blue)("Linear functions are in the form"` `color(blue)(f(x)=ax+b`

`"Where"` `x` `"is the variable"`

`color(blue)("There is only one variable"`

`color(blue)("The highest power of the variable is 1"`

Now we can check whether these equations are linear equations

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(red)(4y+2x^2=20`

graph{4y+2x^2=20}

This is not a linear equation as you can see

`*`It does not show a straight line when graphed

`*`It is not in the form `ax+b`

`*`There are `2` variables instead of `1`

`*`The highest power of the variable is not `1`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(red)(x^2+y=-9`

graph{x^2+y=-9}

This is not a linear equation as you can see

`*`It does not show a straight line when graphed

`*`It is not in the form `ax+b`

`*`There are `2` variables instead of `1`

`*`The highest power of the variable is not `1`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

So,these are not linear functions