How do you determine the intersection between parametric curves #(t^2+2t,-3t^2+5t)# and #(-2t^2+4t,t^2+2t)#?

Question

As mentioned in the title, I have the following parametric curves:

Red: #(t^2+2t,-3t^2+5t)#
Blue: #(-2t^2+4t,t^2+2t)#

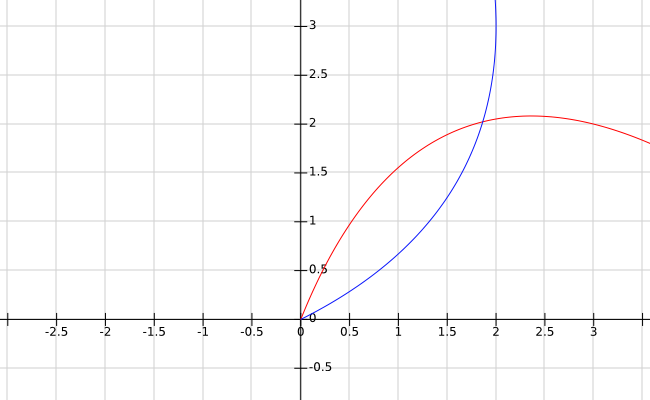
I have tried to write the curves in function form using the method that PatrickJMT demonstrates, but I encountered two #+-# symbols in the same equation, and I am unsure how to proceed.

How do I find the exact intersections?

Thanks!

5558 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-08T15:58:56

See below.

Defining

#f_1(x(t),y(t))={t^2 + 2 t, -3 t^2 + 5 t}# and
#f_2(x(t),y(t))={-2 t^2 + 4 t, t^2 + 2 t}#

We can verify that the set of coincidence points only has one element: The point #(0,0)# at the instant #t = 0#.

The functions

#f_1(x,y)# and #f_2(x,y)# have crosses in two points:

#{0,0}# and #{ 1.8636, 2.02359}#

Those points are the solutions of the nonparametric curves

#f_1(x,y)=sqrt[1 + x] - 1/6 (5 - sqrt[25 - 12 y])-1=0# and
#f_2(x,y)=1/2 (2 - sqrt[2] sqrt[2 - x]) - ( sqrt[1 + y]-1)=0#