How do you find the exact value of #(sin30)^2+(cos30)^2#?
1 Answer
Nov 4, 2016
The expression equals
Explanation:
Consider the special triangle below.
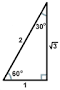
We start by defining sine and cosine.
So,
We can now calculate the value of
Note that we could also have used the pythagorean identity
Hopefully this helps!

