Question

A parallelogram has sides with lengths of `24` and `9`. If the parallelogram's area is `135`, what is the length of its longest diagonal?

Answer 1

`31.53`

Explanation:

With these types of questions, it's better to draw a symbolic geometric shape, in this case, a parallelogram. After drawing the parallelogram, draw the two diagonals. You'll see that the longest diagonal is to the opposite side of the obtuse angle. After determining the longest diagonal, you can erase the other diagonal.

Now there should be two triangles in the parallelogram like this;

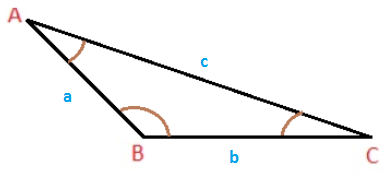
Consider `b=24` , `a=9` and `c` the diagonal we want to find.
This triangle has an area that is half of the parallelogram which is `135/2=67.5`
In order to find `c`, we need to find the angle `B`. Using the sine area theorem, which is `1/2*a*b*sinB=A(ABC)` in this triangle;

`1/2*24*9*sinB=67.5`

`sinB=0.625`

`B~~141.32` degrees

Now we know the angle `B`, we can find `c` by using the cosine theorem, which would be `c^2= a^2+b^2-2*a*b*cosB` in this triangle.

`c^2 = 24^2+9^2-2*24*9*cosB`

`c^2 ~~ 657 + 432*0.781`

`c^2 ~~ 994.2`

`c ~~ sqrt994.2 ~~ 31.53`