Question

How do you find the equation for the tangent line to `sin^2x` at `x=pi/3`?

Answer 1

`y = 1/2sqrt(3) x +3/4- pi/6sqrt(3)`

Explanation:

Let `y =sin^2x` then we need to find the gradient of the tangent to y when `x=pi/3`, which means we need to find the derivative and find `dy/dx` when `x=3`

If we differentiate wrt `x'` using the chain rule we have:
`y =sin^2x`
`:. dy/dx =2sinxcosx`
`:. dy/dx =sin(2x)` (as sin2A-=2sinAcosA)

So, When `x=pi/3 => dy/dx=sin(2pi)/3 =1/2sqrt3`

Also, When `x=pi/3 => y=sin^2pi/3 = (1/2sqrt3)^2=3/4`

So the tangent passes through `(pi/2, 3/4)` and has gradient `m=1/2sqrt3`

If you use the equation `y-y_1=m(x-x_1)` then the tangent equation is:
`y - 3/4 = 1/2sqrt(3) x - pi/3 )`
`:. y - 3/4 = 1/2sqrt(3) x - pi/6sqrt(3)`
`:. y = 1/2sqrt(3) x +3/4- pi/6sqrt(3)`

Answer 2

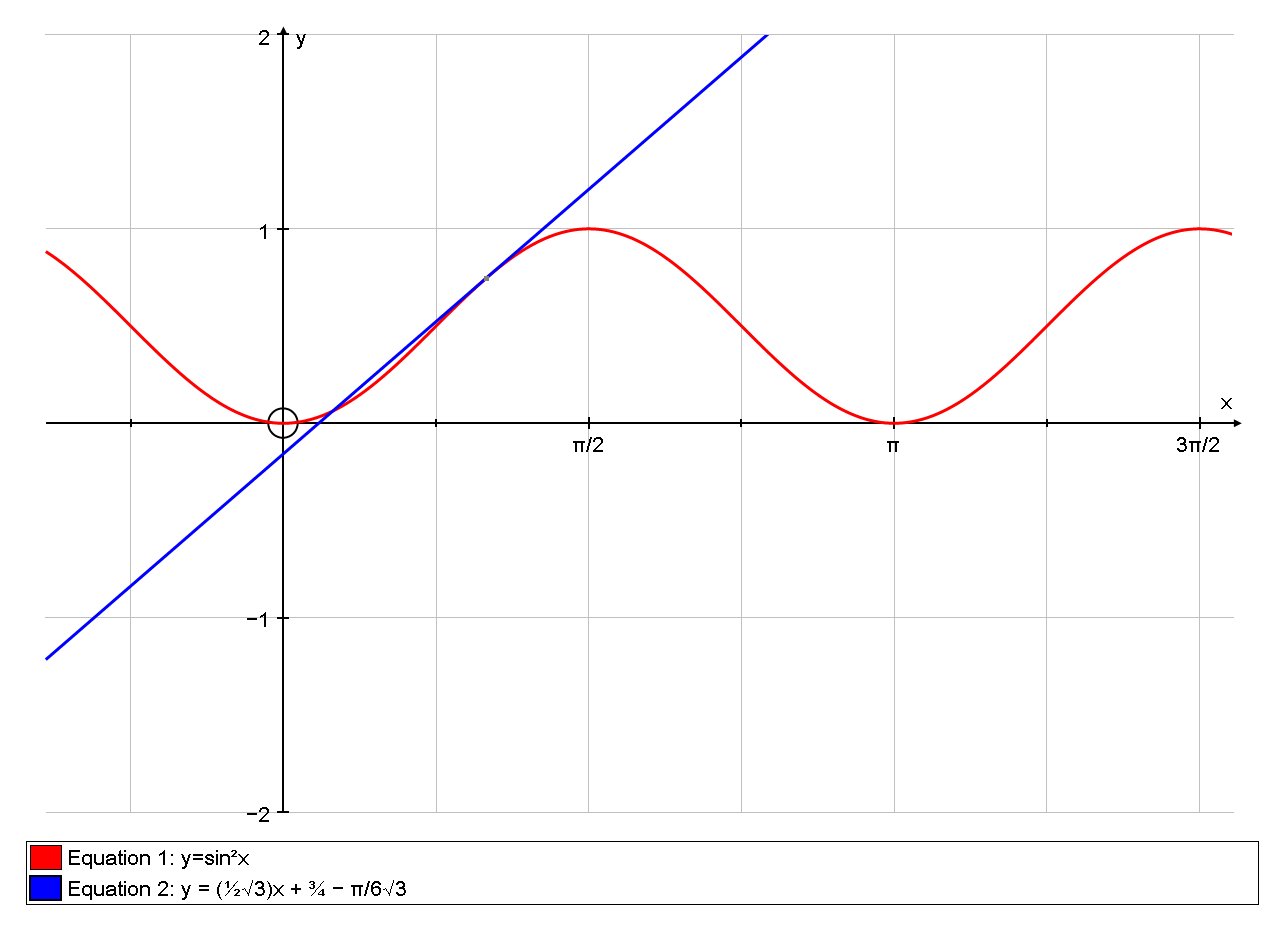
Start by finding the corresponding y-coordinate that the tangent passes through.

`y = sin^2(pi/3) =(sqrt(3)/2)^2 = 3/4`

Now, determine the derivative.

`y = sin^2x -> y = (sinx)(sinx)`

`y' = cosx xx sinx + cosx xx sinx`

`y' = cosxsinx + cosxsinx`

`y' = 2cosxsinx`

`y' = sin2x`

We can find the slope of the tangent.

`m_"tangent" = sin((2pi)/3) = sqrt(3)/2`

Next, find the equation of the tangent.

`y - y_1 = m(x- x_1)`
`y - 3/4 = sqrt(3)/2(x - pi/3)`

`y - 3/4 = sqrt(3)/2x - (pisqrt(3))/6`

`y = sqrt(3)/2x - (pisqrt(3))/6 + 3/4`

`y = sqrt(3)/2x - (2pisqrt(3) - 3)/12`

Hopefully this helps!