Question #e31c1
1 Answer
Please see the explanation.
Explanation:
Here is a graph of the 3 boundaries:
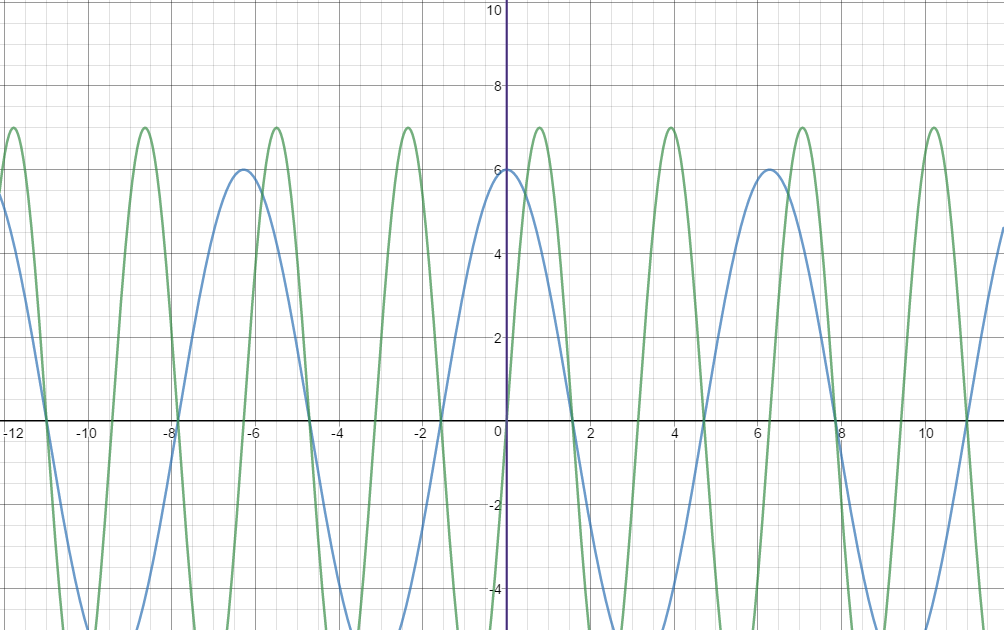
Decide whether to integrate
You want to find the area between the y axis and green curve until it intersects with the blue curve. At first, you might want to do it with respect to y but you will be integrating inverse sine and inverse cosine function. I say no. I think that it is easier to find the area of the same region as the difference between the functions with respect to x.
Find the limits of integration:
We know that we want to start integrating from
Use
Here is your integral is:
I hope that this helps.
