What particle is needed to complete this nuclear reaction? #"_86^222Rn##->##"_84^218 Po + underline# ?
1 Answer
An alpha particle.
Explanation:
The thing to remember about nuclear equations is that mass and charge must always be conserved.
In other words, in any nuclear equation
- the overall mass number remains unchanged
- the overall atomic number remains unchanged
Your unbalanced nuclear equation looks like this
#""_ (color(white)(1)color(blue)(86))^color(darkgreen)(222)"Rn" -> ""_ (color(white)(1)color(blue)(84))^color(darkgreen)(218)"Po" + ""_ (color(blue)(Z))^color(darkgreen)(A)"?"#
The goal here is to find the atomic number,
Since the overall mass number must be conserved, you can say that
#color(darkgreen)(222) = color(darkgreen)(218) + color(darkgreen)(A) -># conservation of mass
This will get you
#color(darkgreen)(A) = 222 - 218 = 4#
The overall atomic number is also conserved, so you can say that
#color(blue)(86) = color(blue)(84) + color(blue)(Z)#
This will get you
#color(blue)(Z) = 86 - 84 = 2#
The unknown particle has a mass number equal to
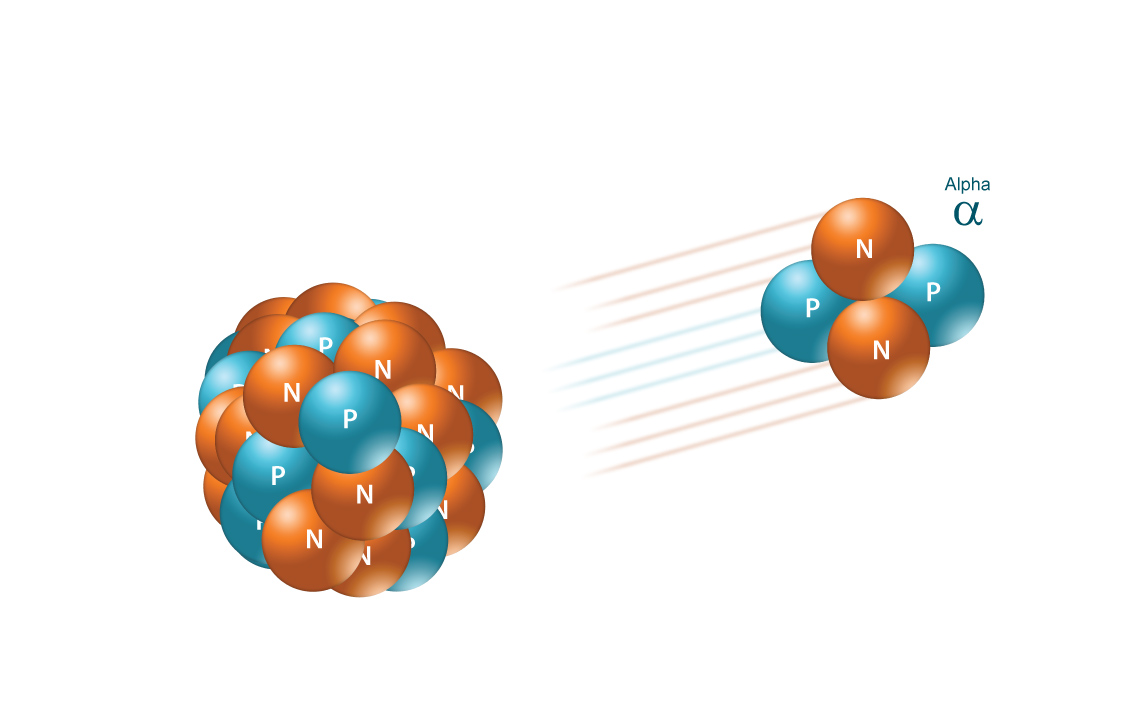
In essence, an alpha particle is simply the nucleus of a helium-4 atom, i.e. it contains
You can now complete the nuclear equation that describes the alpha decay of radon-222 to polonium-218
#""_ (color(white)(1)86)^222"Rn" -> ""_ (color(white)(1)84)^218"Po" + ""_ 2^4alpha#

