Question

A rectangle is inscribed with its base on the x axis and its upper corners on the parabola y = 12 − x^2. What are the dimensions of such a rectangle with the greatest possible area?

Answer 1

The greatest area occurs when the rectangle has a width of 4 and a height of 8 leading to a maximum area of 32

Explanation:

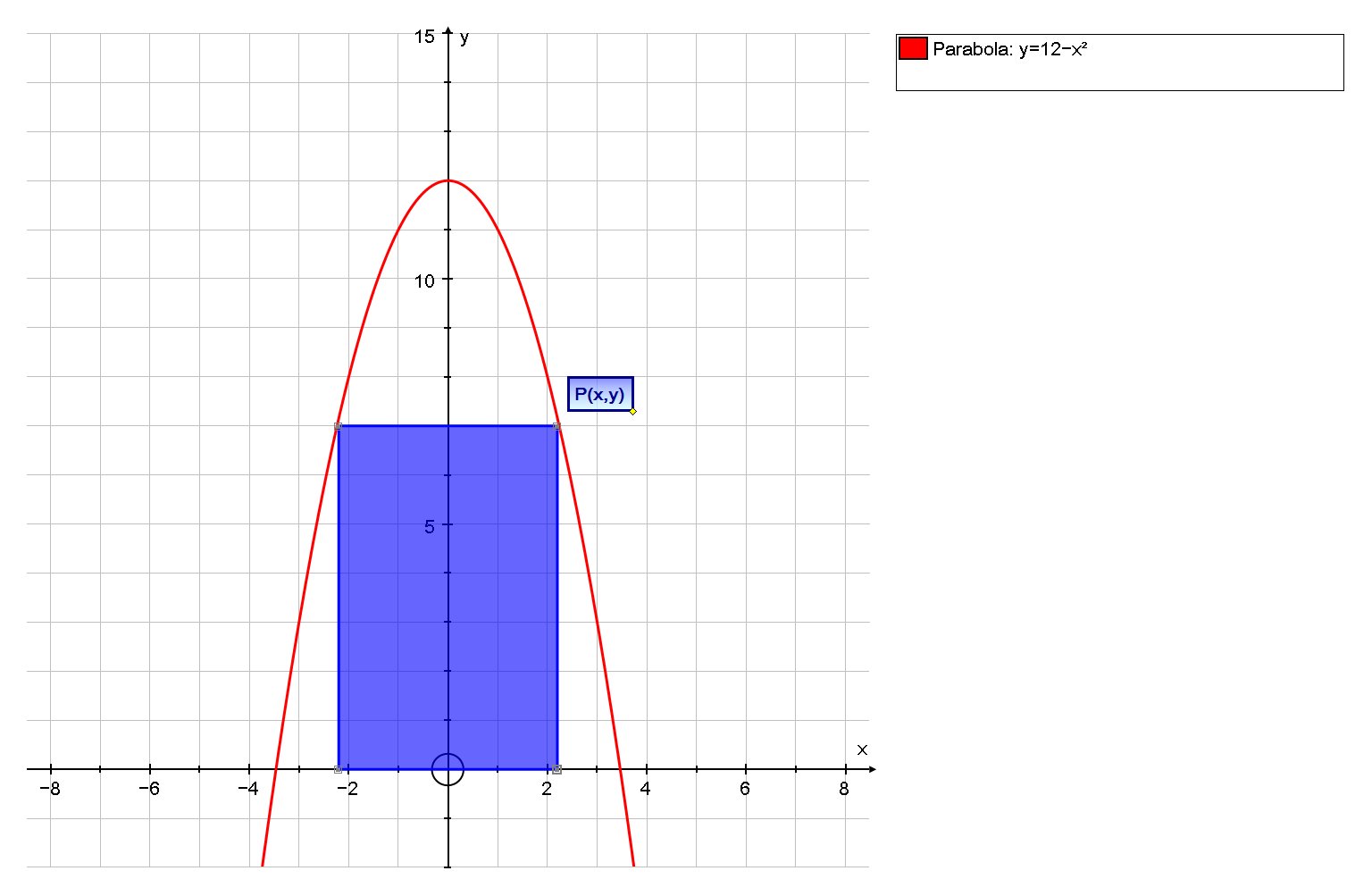
Let us set up the following variables:

`{(P(x,y), "coordinate of the right hand corner"), (A, "Area of Rectangle") :}`

`P` lies on the parabola and `y=12-x^2`, so `P=P(x,12-x^2)`

Due to symmetry The width of the rectangle is half the distance between P and the y-axis, ie

Width = `2x` and Height=`y`

Hence the Area of the rectangle is:

`\ \ \ \ \ A = Wdith xx Height`
`:. A = 2xy`
`:. A = 2x(12-x^2)`
`:. A = 24x-2x^3)` ..... [1]

We are asked to maximise the Area as `x` changes so hopefully we can identify a critical point of `A` associated with a maximum, So we need to find `(dA)/dx`

Differentiating [1] wrt `x`
`:. (dA)/dx = 24-6x^2` ..... [2]

At a critical point, `(dA)/dx = 0`

`:. 24-6x^2 = 0`
`:. 6x^2 = 24`
`:. x^2 = 4`
`:. x = +-2`

Obviously `x` must be positive (otherwise we have an imaginary rectangle with negative area for a box that has collapsed in on itself)

`:. x = 2`

We need to check if this is a max or a min, so differentiate [2] wrt `x` to get;

`:. (d^2A)/dx^2 = -12x`
`:. (d^2A)/dx^2 = -12x < 0 " when " x=2`, confirming a max

When `x=2` we have:

Width = `2*2 = 4`
Height = `12-4=8`
Area = `32`