Question

Assume the bottom of a 16 ft ladder is pulled out at a rate of 3 ft/s. How do you find the rate at the top of the ladder when it is 10 ft from the ground?

Answer 1

It is sliding down at a rate of `3.75` ft/sec

Explanation:

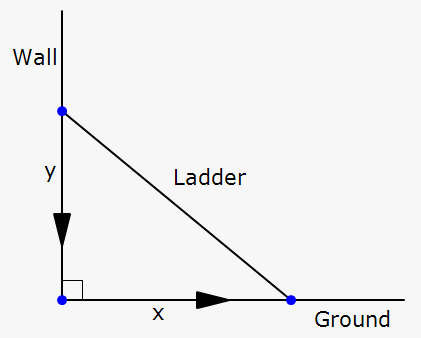
Let us define the following variables:

`{(x, "Distance of bottom of ladder from the wall (ft)"), (y, "Distance of top of ladder from the floor (ft)") :}`

We are told that `dx/dt=3 " ft/s"` and we aim to find `dy/dt` when `y=10`

The ladder is a fixed length (`16 ft`) so by Pythagoras;

`x^2+y^2=16^2`
`:. x^2+y^2=256`

Differentiating Implicitly wrt `t` we get:

`2xdx/dt + 2ydy/dt=0`
`:. 2x*3 + 2ydy/dt=0`
`:. 3x + ydy/dt=0`

When `y=10 => x^2+100=256`

`:. x^2=156`
`:. x=sqrt(156) " as " (x >0)`

And so substituting `x=sqrt(156), y=10` into our derivative gives:

`3sqrt(156) + 10dy/dt=0`
`:. dy/dt = -3/10sqrt(156)`
`:. dy/dt = -3.74699 ...`
`:. dy/dt = -3.75 (2dp)`

The minus sign denotes that the ladder is sliding down, i.e., the height `y` is decreasing. It is sliding down at a rate (speed) of `3.75` ft/sec