Question

How do you find the focus, directrix and sketch `y=1-x-x^2`?

Answer 1

Please see the explanation.

Explanation:

Write the equation in the form `y = ax^2 + bx - c`:

`y = -x^2 - x + 1`

We observe that `a = -1, b = -1, and c = 1`

The x coordinate, h, of the vertex and the focus can be found using the equation:

`h = -b/(2a)`

Substitute -1 for b and -1 for a:

`h = -1/2`

The y coordinate, k, of the vertex can be found by evaluating the function at `x = h = -1/2`:

`k = -1/4 + 1/2 + 1`

`k = 5/4`

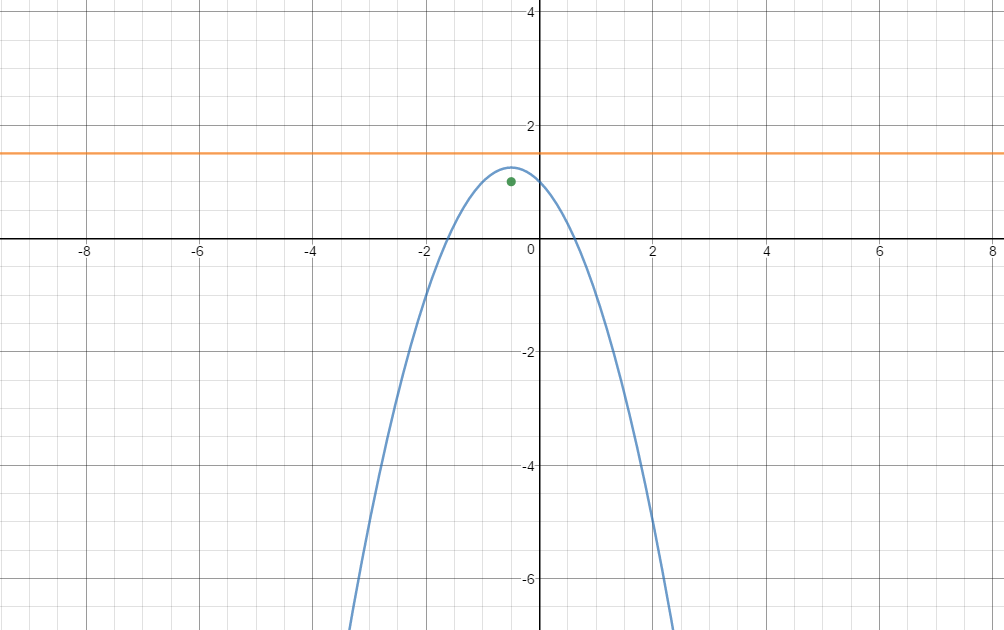
The vertex is at `(-1/2,5/4)`

The y distance, f, from vertex to the focus can be found using the equation:

`f = 1/(4a)`

`f = -1/4`

Add `-1/4` to the y coordinate of the vertex to obtain the y coordinate of the focus and the x coordinates are the same:

The focus is at `(-1/2, 1)`

The directrix is a horizontal line the same distance on the other side of the vertex:

`y = 5/4 + 1/4`

The directrix is:

`y = 3/2`

Here is a graph of the parabola, the focus, and the directrix: