How do you find the quadratic function with vertex (5,12) and point (7,15)?
1 Answer
Please see the explanation.
Explanation:
There are two equations that can be written.
- Uses the vertex form:
#y = a(x - h)^2 + k#
where h and k correspond to the vertex point#(h, k)# and you solve for a using the specified point. - Uses the vertex form:
#x = a(y - k)^2 + h#
where h and k correspond to the vertex point#(h, k)# and you solve for a using the specified point.
Substitute the vertex
Using the specified point
Solve for for a :
Substitute
Here is a graph showing that both equations [3] and [4] have the specified vertex and pass through the specified point:
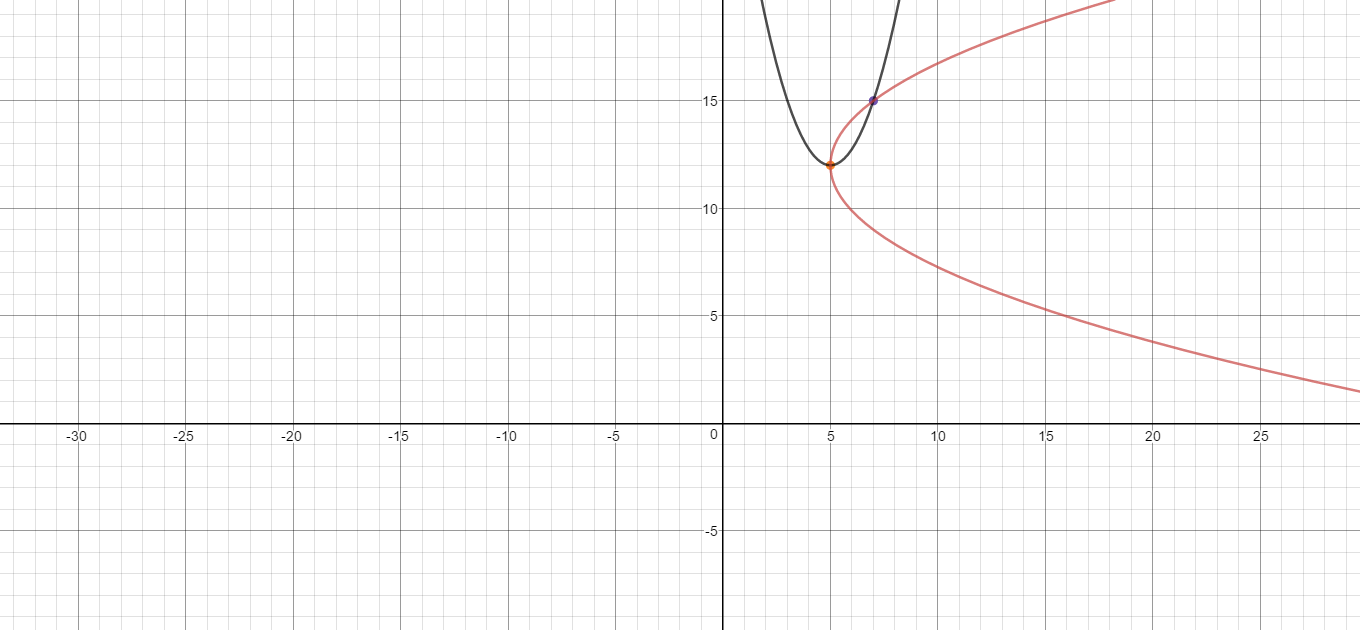
However, you asked for a function, Equation [3] is the only function. Equation [4] is not a function.
