A triangle has corners at points A, B, and C. Side AB has a length of #16 #. The distance between the intersection of point A's angle bisector with side BC and point B is #9 #. If side AC has a length of #18 #, what is the length of side BC?
1 Answer
Jan 9, 2017
Explanation:
Let us draw the figure as given below:
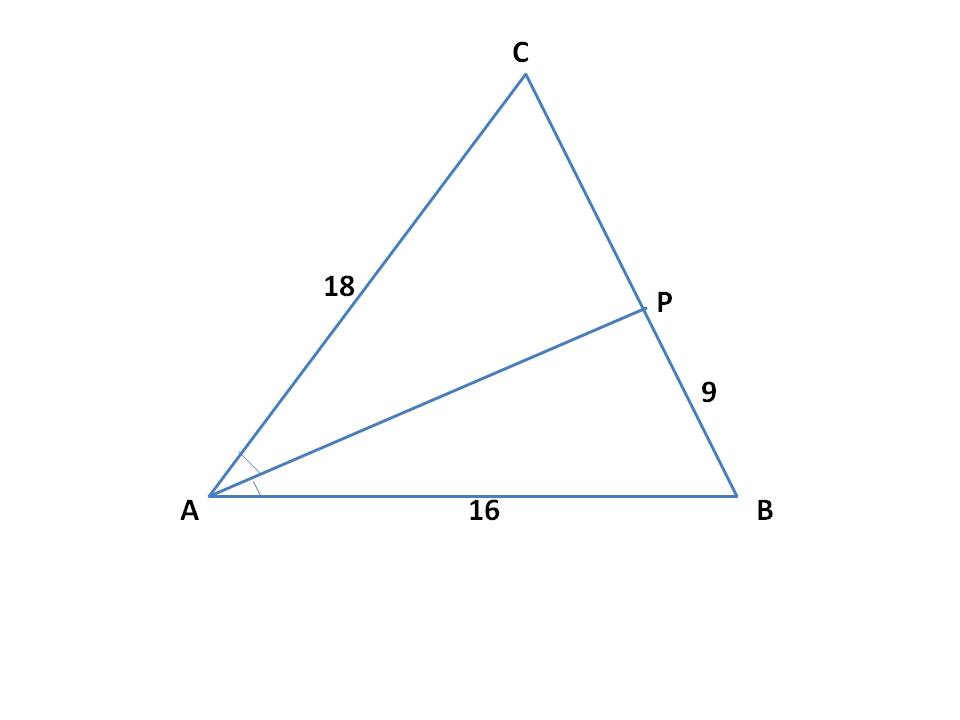
Here
Now as
Hence
