Question

An object with a mass of `4 kg` is on a plane with an incline of `- pi/8`. If it takes `18 N` to start pushing the object down the plane and `15 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

The static coefficient of friction is `0.9112` (4dp)
The kinetic coefficient of friction is `0.8284` (4dp)

Explanation:

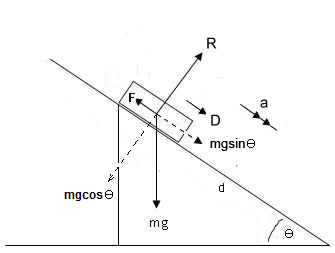
For our diagram, `m=4kg`, `theta=pi/8`

If we apply Newton's Second Law up perpendicular to the plane we get:

`R-mgcostheta=0`
`:. R=4gcos(pi/8) \ \ N`

Initially it takes `18N` to start the object moving, so `D=18`. If we Apply Newton's Second Law down parallel to the plane we get:

`D+mgsin theta -F = 0`
`:. F = 18+4gsin (pi/8) \ \ N`

And the friction is related to the Reaction (Normal) Force by

`F = mu R => 18+4gsin (pi/8) = mu (4gcos(pi/8))`
`:. mu = (18+4gsin (pi/8))/(4gcos(pi/8))`
`:. mu = 0.911230 ...`

Once the object is moving the driving force is reduced from `18N` to `15N`. Now `D=15`, reapply Newton's Second Law down parallel to the plane and we get:

`D+mgsin theta -F = 0`
`:. F = 15+4gsin (pi/8) \ \ N`

And the friction is related to the Reaction (Normal) Force by

`F = mu R => 15+4gsin (pi/8) = mu (4gcos(pi/8))`
`:. mu = (15+4gsin (pi/8))/(4gcos(pi/8))`
`:. mu = 0.828394 ...`

So the static coefficient of friction is `0.9112` (4dp)
the kinetic coefficient of friction is `0.8284` (4dp)