Question

A truck pulls boxes up an incline plane. The truck can exert a maximum force of `3,500 N`. If the plane's incline is `(5 pi )/12` and the coefficient of friction is `7/12`, what is the maximum mass that can be pulled up at one time?

Answer 1

Maximum mass is `438.24 \ kg` (2dp)

Explanation:

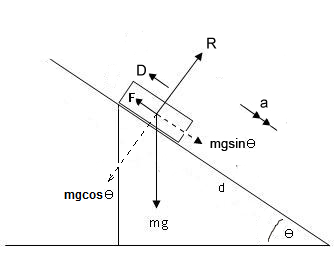
For our diagram, `m="mass "kg`, `theta=(5pi)/12`

If we apply Newton's Second Law up perpendicular to the plane we get:

`R - mg cos theta = 0`
`:. R = mg cos((5pi)/12) \ \ N`

With a maximum driving force of `3500\ N` upwards (along the plane) `D=3500`. If we Apply Newton's Second Law up parallel to the plane we get:

`D + F - mg sin theta = 0`
`:. 3500 +F - mg sin ((5pi)/12) = 0`
`:. F = mg sin ((5pi)/12) - 3500`

And the friction is related to the Reaction (Normal) Force by

`F le mu R`
`:. mg sin ((5pi)/12) - 3500 le 7/12 (mg cos((5pi)/12) )`
`:. 12mg sin ((5pi)/12) - 42000 le 7mg cos((5pi)/12)`
`:. 12mg sin ((5pi)/12) - 7mg cos((5pi)/12) le 42000`
`:. mg(12 sin ((5pi)/12) - 7 cos((5pi)/12)) le 42000`
`:. m le 42000/((12 sin ((5pi)/12) - 7 cos((5pi)/12))g)`
`:. m le 438.2400291 ...`