Question #2d40e
1 Answer
Explanation:
You are asked to find the number of electrons located in a sodium atom that can have the spin quantum number equal to
As you know, the spin quantum number,
# m_s = +1/2 -># the electron has spin-up#m_s = -1/2 -># the electrons has spin-down
Now, an orbital can hold a maximum of
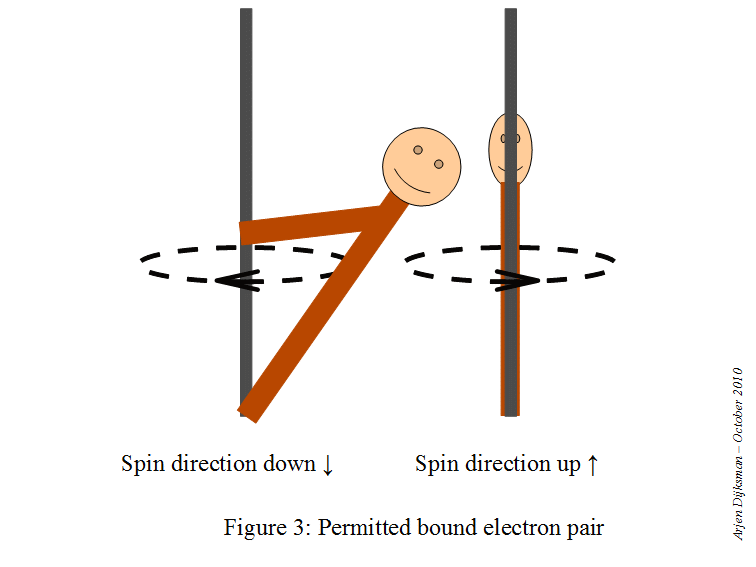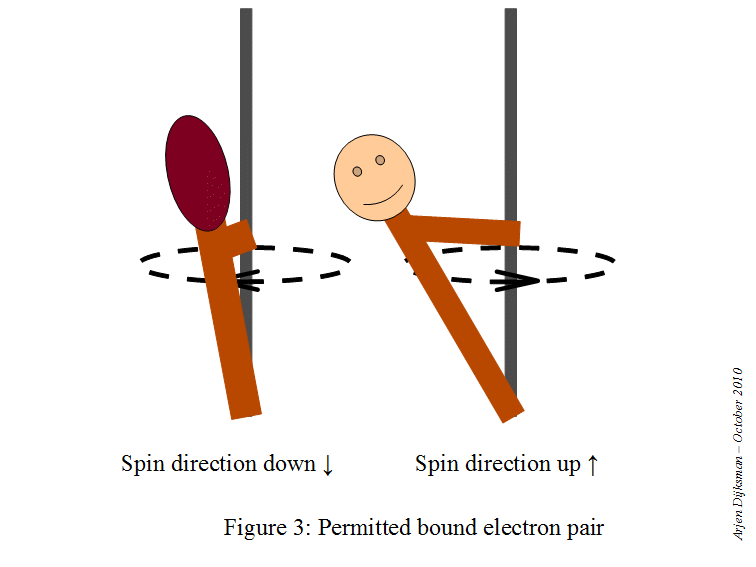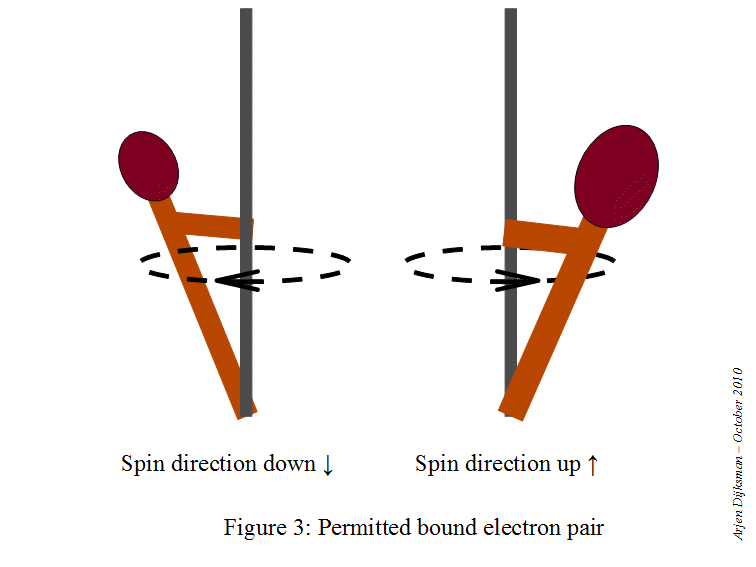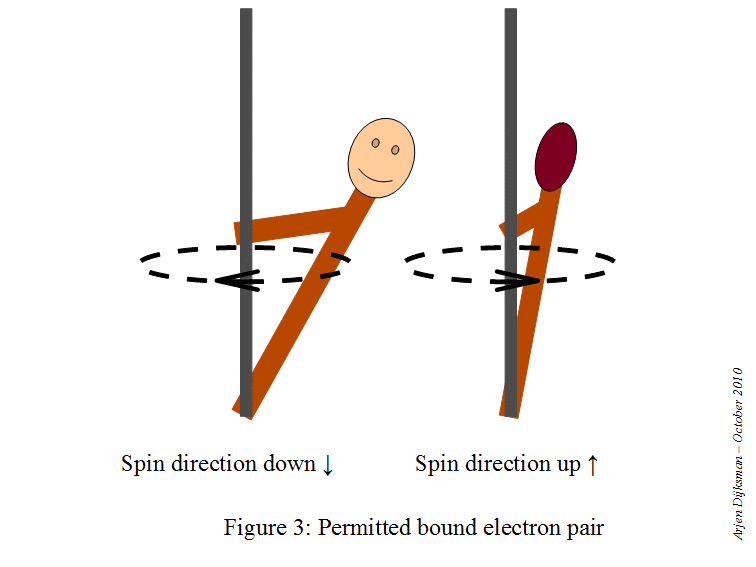
This means that a starting point here would be to write the electron configuration for a neutral sodium atom and look for orbitals that are completely filled, since you know that
#color(red)(ul(color(black)("1 fully-occupied orbital" -> "1 electron with m"_s = +1/2)))#
The electron configuration for a neutral sodium atom looks like this -- for neutral atoms, the atomic number, which gives you the number pf protons located in the nucleus, also gives you the number of electrons that surround the nucleus
#"Na: " 1s^2 2s^2 2p^6 3s^1# Here you have
#Z = 11# , which means that the electron configuration must account for a total of#11# electrons
The electron configuration for a neutral sodium atom features
#1s^2 -># the 1s orbital is completely filled#2s^2 -># the 2s orbital is completely filled#2p^6 = {(2p_x^2), (2p_y^2), (2p_z^2) :} -># all three 2p orbitals are completely filled#3s^1 -># the 3s orbital is only partially filled
So, you know that you have
#"5 fully-occupied orbitals" -> "5 electrons that have m"_s = +1/2#
Now, the
#color(darkgreen)(ul(color(black)("5 e"^(-) + "1 e"^(-) = "6 e"^(-))))#
This is how the electron diagram for a neutral sodium atom would look like.
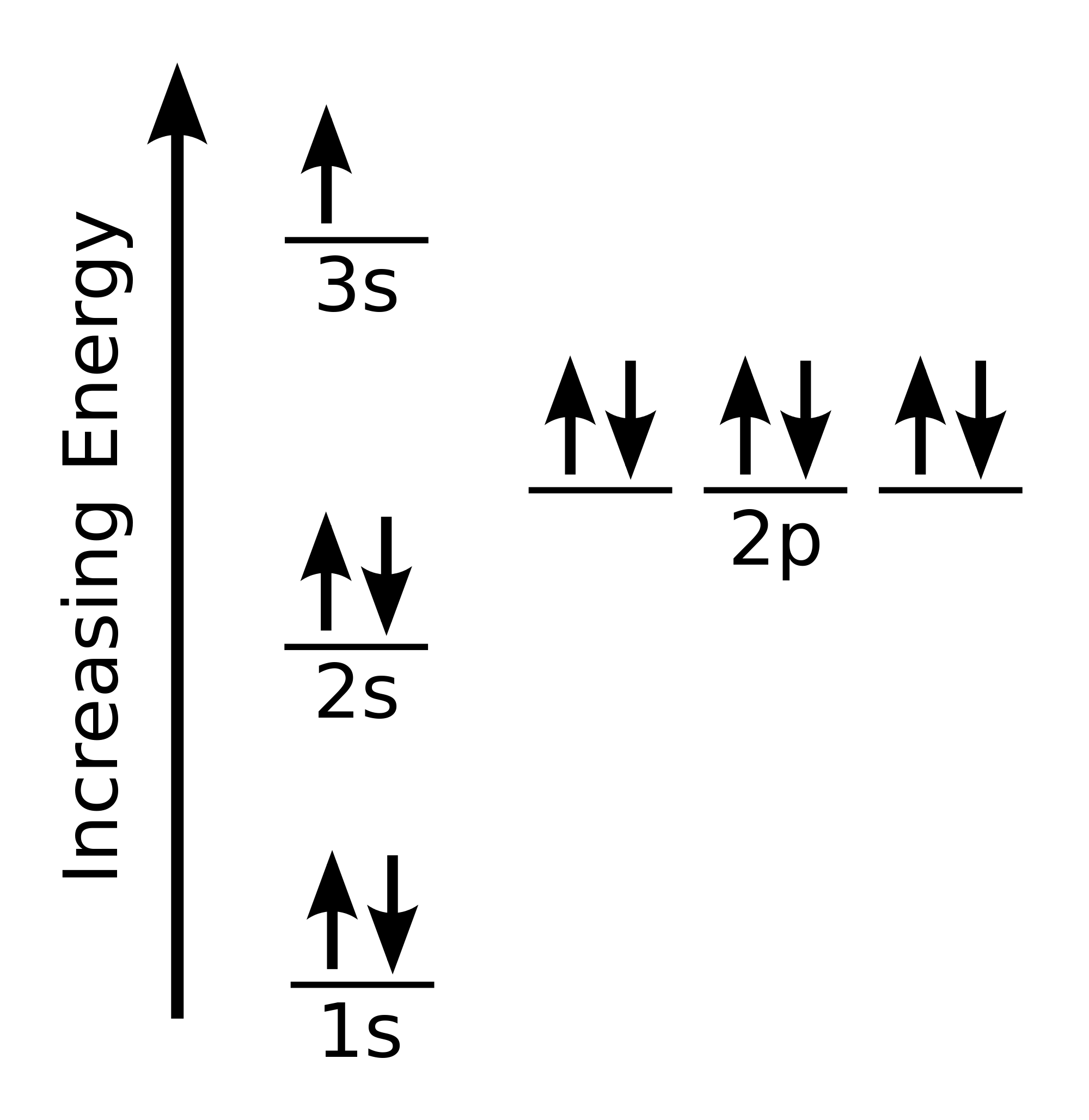
Here the electrons that have
As you can see, if we follow the aforementioned convention, we find that

