Question

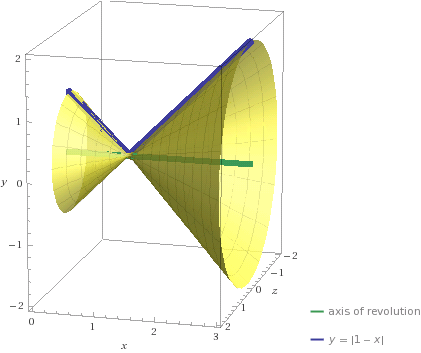
What is the surface area produced by rotating `f(x)=abs(1-x), x in [0,3]` around the x-axis?

Answer 1

`5 sqrt(2) \ pi`

Explanation:

If we look at the graph `y=abs(1-x)` we get:
graph{|1-x| [-10, 10, -5, 5]}

so rotating about )x will produce two cones:

One smaller cone of height `1`, and one larger cone of height `3`,

The surface area of a cone of radius `r` is given by `pi rl` where `l` is the length of the slope:

For the smaller cone:

`l^2=1^2+1^2 => l=sqrt(2)`

For the larger cone:

`l^2=2^2+2^2 => l=sqrt(8) =2sqrt(2)`

So total surface area is:

`SA =(pi)(1)(sqrt(2)) + (pi)(2)(2sqrt(2))`
`\ \ \ \ \ =5 sqrt(2) \ pi`