Question

How To Do These Pythagorean Theorem Math Questions?

Hi all, here are some questions for the past day I am not able to absolutely understand could someone please give me explanations on how to solve these? I will put the pictures below.

This is #9 the question

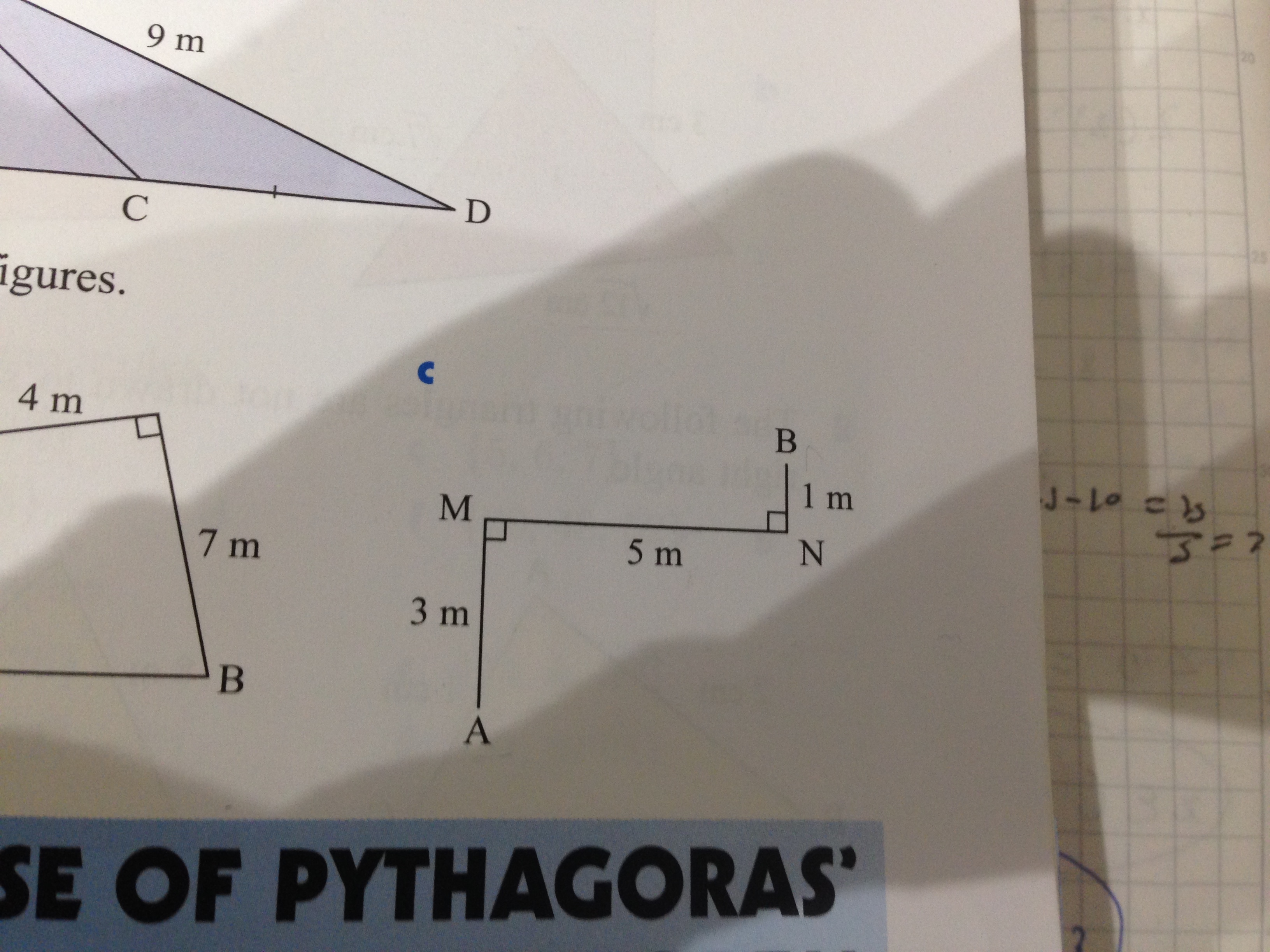
This is #9c I am unable to solve this

This is number `3 and`5 I am unable to solve this

I understand all of you are very busy! If you are able to answer all of these hopefully simple questions, I'd really appreciate it!

Answer 1

Answer to ex. 9c: `AB=sqrt41`
Answer to ex. 3: the perimeter is `24sqrt5` and the area is `160`
Answer to ex. 5: the side of the square is `5sqrt2`

Explanation:

Answer to ex. 9c:

Let C be the intersection of MN with AB:
the triangles AMC and NBC are similar

(`hatM=hatN=90°` and `BhatCN=MhatCA` since they are opposite angles);

let `x=CN` and `5-x=MC`, then it is:

`3/1=(5-x)/x`

that's

`3x=5-x`

`4x=5`

`x=5/4 ->CN=5/4`

`MC=5-x=5-5/4=15/4`

Then AB=AC+BC and, by the Pythagoras theorem, it is:

`AB=sqrt(3^2+(15/4)^2)+sqrt((5/4)^2+1^2)`

`=sqrt(9+225/16)+sqrt(25/16+1=`

`=sqrt(369/16)+sqrt(41/16)`

`=3/4sqrt(41)+1/4sqrt(41)`

`=sqrt41`

Answer to ex.3

Let x the lower side of the rectangle, then the greater one will be 2x, then let's solve the equation:

`x^2+(2x)^2=20^2` (Pythagoras theorem)

`x^2+4x^2=400`

`5x^2=400`

`x^2=80`

`x=sqrt(80)=4sqrt5` (the lower side)

`2x=8sqrt5` (the second side)

Then the perimeter is:

`2*4sqrt5+2*8sqrt5=8sqrt5+16sqrt5=24sqrt5`

and the area is:

`4sqrt5*8sqrt5=32*5=160`

Answer to ex. 5

In a square the relation between side and diagonal is:

diagonal=side`*sqrt2`

Then side=diagonal`/sqrt2=10/sqrt2=10sqrt2/2=5sqrt2`

Answer 2

`AB=6.403`

Explanation:

Please see the diagram below for reference.

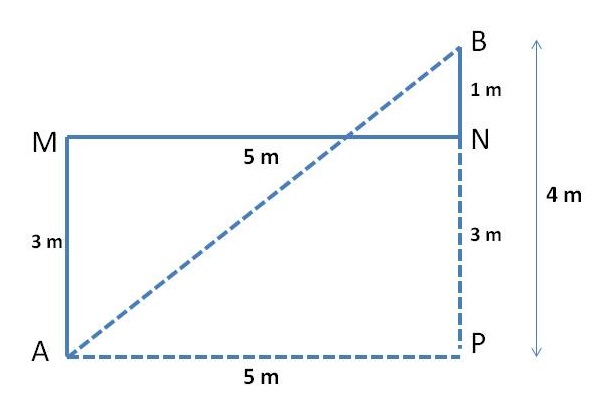
Here we have extended `BN` to `P` and draw `AP` perpendicular to `BP`.

Now as `APNM` is a rectangle, `MA=NP=3` `m` and hence `BP=1+3=4` `m`

Similarly `AP=MN=5` `m`

Now as `DeltaABP` is a right angled triangle,

`AB^2=BP^2+AP^2=4^2+5^2=16+25=41`

and `AB=sqrt41=6.403`

Answer 3

(3) Perimeter `=24sqrt5cm`
Area `=160cm^2`
(4)Side of square `=5sqrt2cm`
(9)`AB=sqrt41 m`

Explanation:

(3) Let `x=` length of smaller side

Length of other side is `=2x`

Therefore,

`x^2+(2x)^2=20^2`

`x^2+4x^2=400`

`5x^2=400`

`x^2=400/5=80`

`x=sqrt80=sqrt(16*5)=4sqrt5`

Perimeter `=2x+4x=6x=6*4sqrt5=24sqrt5 cm`

Area `=x*2x=2x^2=2*80=160 cm^2`

(5)Let `a=` length of the side of the square

`a^2+a^2=10^2`

`2a^2=100`

`a^2=50`

`a=sqrt50=sqrt(25*2)=5sqrt2`

(9c) Easier way to calculate `AB`

`AB^2=MN^2+(MA+NB)^2`

`AB^2=5^2+(3+1)^2`

`AB^2=25+16=41`

`AB=sqrt41`

Let `O` be the intersection of AB and MN

Let `MO=x`, then `ON=5-x`

Triangles OMA and ONB are similar

Therefore,

`x/3=(5-x)/1`

`x=15-3x`

`4x=15`

`x=15/4`

`AO^2=MA^2+MO^2`

`AO^2=3^2+(15/4)^2=9+225/16=(144+225)/16`

`AO=sqrt369/4`

`NO=5-15/4=5/4`

`OB^2=ON^2+BN^2`

`=(5/4)^2+1=25/16+1=41/16`

`OB=sqrt41/4`

Finally,

`AB=AO+OB=sqrt369/4+sqrt41/4`

I hope that this will help!!!