How do you convert #2sinθ-3cosθ=r# to rectangular form?
2 Answers
The answer is
Explanation:
To convert from polar coordinates
Therefore
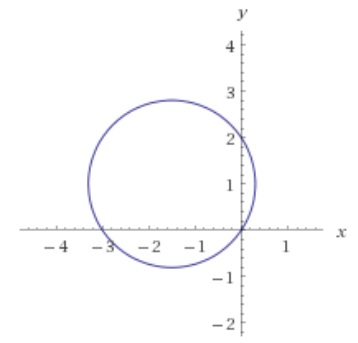
This is the equation of a circle, center
Explanation:
You are given an equation in terms of radius,
#r=sqrt(x^2+y^2)# #sin(theta)=y/r=y/sqrt(x^2+y^2)# #cos(theta)=x/r=x/sqrt(x^2+y^2)# #tan(theta)=y/x#
Now we can replace the
Multiply both sides of the equation by
Solving for
The graph of this is a circle