a). Rate expression
The total volume in each experiment is the same: 50 mL.
Hence, the concentrations of #"KI"# and #"Fe"^"3+"# are directly proportional to their volumes.
We can't get the order with respect to #"KI"# because its concentration is always the same.
However, we can get the order with respect to #"Fe"^"3+"#.
We are given
#y ∝ ["Fe"^"3+"]^x# and
#y ∝ 1/t["Fe"^"3+"]^x#
∴ #y ∝ 1/t# or #y = k/t#
From Experiments 1 and 2, it appears that doubling the concentration halves the time (doubles the rate).
Thus the reaction appears to be first order in #["Fe"^"3+"]#.
Hence, the rate expression is #r = k["Fe"^"3+"]^1# or #r = k["Fe"^"3+"]#.
(b) Plot of concentration vs #1/t#
If a plot of rate (#1/t#) vs concentration (#x#) is a straight line, the reaction is first order in #["Fe"^"3+"]#.
We have the following data:
#bb("Expt."color(white)(m)x//"cm"^3color(white)(m) t color(white)(mml)1//t)#
#color(white)(m)1color(white)(mmmml)5color(white)(mm)92color(white)(mm)0.0109#
#color(white)(m)2color(white)(mmmll)10color(white)(mm)45.4color(white)(ml)0.0220#
#color(white)(m)3color(white)(mmmll)15color(white)(mmll)?color(white)(mmm)?#
#color(white)(m)4color(white)(mmmll) 20color(white)(mm)23color(white)(mml)0.0435#
#color(white)(m)5color(white)(mmmll)25color(white)(mm)18.1color(white)(ml)0.0552#
We plot #1/t# vs #x# and get a graph that looks like this:
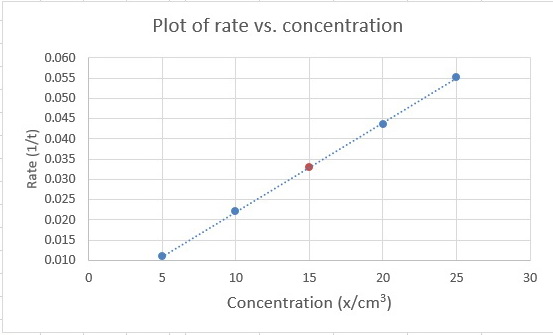
You are given that the equation for the line is #y = kx#, so #k# is the slope of the graph.
The points at #"5 cm"^3# and #"25 cm"^3# appear to be on the line, so we will use them to calculate the slope.
#"Slope" = (Δy)/(Δx) = (y_2-y_1)/(x_2-x_1) = (0.0552 - 0.0109)/("25 cm"^3 - "5 cm"^3) = 0.0443/("20 cm"^3) = 2.22 × 10^"-3"color(white)(l) "cm"^"-3"#
Thus, the rate expression from the graph is
#r = 2.22 × 10^"-3"color(white)(l) "cm"^"-3" × ["Fe"^"3+"]#.
Since #r# is directly proportional to #["Fe"^"3+"]#, the reaction is first order.
The calculated value of #1/t# for #y = "15 cm"^3# is
#1/t = 2.22 × 10^"-3" color(red)(cancel(color(black)("cm"^"-3"))) × 15 color(red)(cancel(color(black)("cm"^3))) = 0.0333#
(I have shown it as a brown point on the line.)
∴ #t = 1/0.0333 = 30.0#


