A parallelogram has sides with lengths of #24 # and #9 #. If the parallelogram's area is #9 #, what is the length of its longest diagonal?
1 Answer
Longest diagonal:
Explanation:
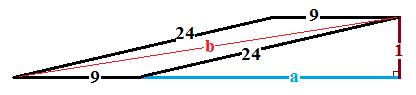
Since the area is given as
the height of the parallelogram must be
Taking the extension of the base to a point perpendicularly below the opposite vertex of the parallelogram and denoting the length of this extension as
by the Pythagorean Theorem
Denoting the longest diagonal as
and re-applying the Pythagorean Theorem using the base plus its extension (
We can use a calculator to derive the approximation
