Solve the equation #z^4+81i=0#?
1 Answer
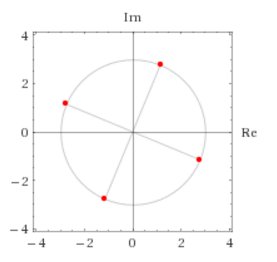
There are four solutions;
# z = 3(-sqrt(2-sqrt(2))/2-sqrt(2+sqrt(2))/2i) #
# z = 3(sqrt(2+sqrt(2))/2-sqrt(2-sqrt(2))/2i) #
# z = 3(sqrt(2-sqrt(2))/2+sqrt(2+sqrt(2))/2i) #
# z = 3(-sqrt(2+sqrt(2))/2+sqrt(2-sqrt(2))/2i) #
Explanation:
Let
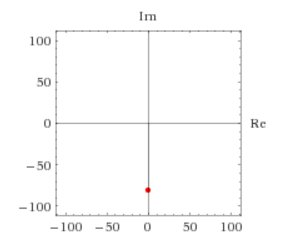
First let us plot the point
And we will put the complex number into polar form (visually):
# |omega| = 81 #
# arg(omega) = -(pi)/2 #
So then in polar form we have:
# omega = 81(cos(-(pi)/2) + isin(-(pi)/2)) #
We now want to solve the equation for
# z^3 = 81(cos(-(pi)/2) + isin(-(pi)/2)) #
Whenever dealing with complex variable equation such as this it is essential to remember that the complex exponential has a period of
# x^3 = 81cos(2npi-(pi)/2) + isin(2npi-(pi)/2)) \ \ \ n in ZZ #
By De Moivre's Theorem we can write this as:
# z = {cos(2npi-(pi)/2) + isin(2npi-(pi)/2)}^(1/4)#
# \ \ = {81}^(1/4){cos(2npi-(pi)/2) + isin(2npi-(pi)/2)}^(1/4)#
# \ \ = 3{cos((2npi-(pi)/2)/4) + isin((2npi-(pi)/2)/4)}#
# \ \ = 3(cos theta + isin theta) #
Where:
# theta = (2npi-(pi)/2)/4 #
# \ \ = 1/8(4n-1)pi #
Put:
# n=-1 => theta = (-5pi)/8 #
# " " :. z = 3(cos ((-5pi)/8)+ isin ((-5pi)/8)) #
# " " :. z = 3(-sqrt(2-sqrt(2))/2-sqrt(2+sqrt(2))/2i) #
# n=0 => theta = (-pi)/8 #
# " " :. z = 3(cos ((-pi)/8)+ isin ((-pi)/8)) #
# " " :. z = 3(sqrt(2+sqrt(2))/2-sqrt(2-sqrt(2))/2i) #
# n=1 => theta = (3pi)/8 #
# " " :. z = 3(cos ((3pi)/8)+ isin ((3pi)/8)) #
# " " :. z = 3(sqrt(2-sqrt(2))/2+sqrt(2+sqrt(2))/2i) #
# n=2 => theta = (7pi)/8 #
# " " :. z = 3(cos ((7pi)/8)+ isin ((7pi)/8)) #
# " " :. z = 3(-sqrt(2+sqrt(2))/2+sqrt(2-sqrt(2))/2i) #
After which the pattern continues.
We can plot these solutions on the Argand Diagram