If #cos x=11/12# then find the value of #tan2x#?
2 Answers
Explanation:
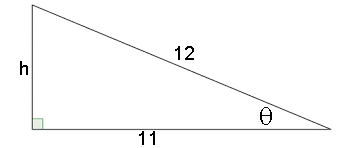
Consider the following right angle triangle:
By elementary trigonometry we have:
# cos theta = "adj"/"hyp" = 11/12 => theta = x #
By Pythagoras:
# \ \ \ 12^2 = 11^2+h^2 #
# :. h^2 = 144-121 #
# :. h^2 = 23 #
# :. \ \h = sqrt(23) #
And so;
# tan x = "opp"/"adj" = h/11 = sqrt(23)/11 #
Using the identity
For comparison, to verify the solution, if we use a calculator:
# \ \ \ \ \ \ \ cos x = 11/12 => x = 23.556^o #
# :. tan 2x= 1.0766 # ; and# (11sqrt(23))/49 = 1.0766 #
Explanation:
Use the identity
Use now the identity:
so:
Then: