Question

Question #6074d

Answer 1

see explanation below

Explanation:

in quadrant 2, the value of #x-axis is -ve while y-axis is +ve and it hypotenuse is +ve value.

sin = y-axis/hypotenuse = +ve value.

cosec = 1/sin = hypotenuse/y-axis = +ve value.

the rest are involve with the #x-axis and become -ve value.

Answer 2

It has to do with the signs of the x and y axis in the second quadrant.

We let `sintheta= b/r`, `costheta = a/r` and `tantheta = b/a`, where `a^2 + b^2 = r^2`. Here's why:

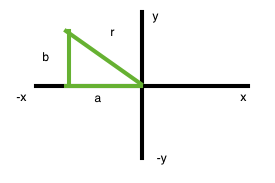
The green triangle is right because side `b` is parallel to the y-axis and the x and y axis are perpendicular to each other. The hypotenuse will always be positive, so it's `a` and `b` that will influence the sign of the ratio.

We have `sintheta = "opposite"/"hypotenuse" = b/r` and `b` will be positive because the y-axis in quadrant II is positive. Therefore, sine will always be positive in quadrant `II`. This also applies to cosecant because `cscx = 1/sinx`.

Hopefully this helps!