What is the angle between electron groups in the tetrahedral geometry?
1 Answer
This can be geometrically worked out, but we expect an angle of
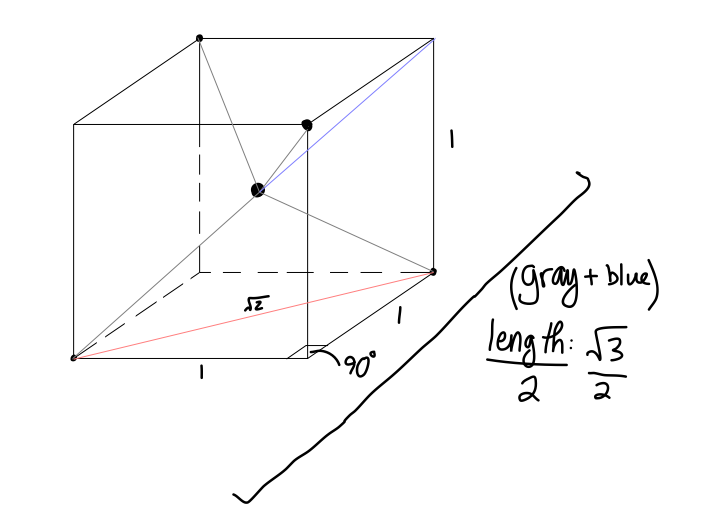
Here,
- the center of the cube is the central atom in a tetrahedral molecule.
- the upper left rear, upper right front, bottom left front, and bottom right rear points are the surrounding atoms in a tetrahedral molecule.
The base diagonal is
#1^2 + (sqrt2)^2 = c^2#
#=> c = sqrt3#
We want half that diagonal, as that is the length towards the central atom in a tetrahedral molecule, so
Finally, we have an
- upper-left:
#x = sqrt3/2# - upper-right:
#y = sqrt3/2# - base diagonal:
#z = sqrt2#
The law of cosines is:
#z^2 = x^2 + y^2 - 2xycosZ#
We can use this to find the tetrahedral angle,
#(z^2 - x^2 - y^2)/(-2xy) = cosZ#
#=> color(blue)(Z) = arccos((z^2 - x^2 - y^2)/(-2xy))#
#= arccos(((sqrt2)^2 - (sqrt3/2)^2 - (sqrt3/2)^2)/(-2(sqrt3/2)(sqrt3/2)))#
#= arccos((2 - 3/4 - 3/4)/(-3/2))#
#= color(blue)(109.5^@)#

