If a 12.0-g sample of radon-222 decays so that after 19 days only 0.375 g remains, what is the half-life of radon-222?

Question

3360 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-26T16:19:43

The half life is #=3.8# days

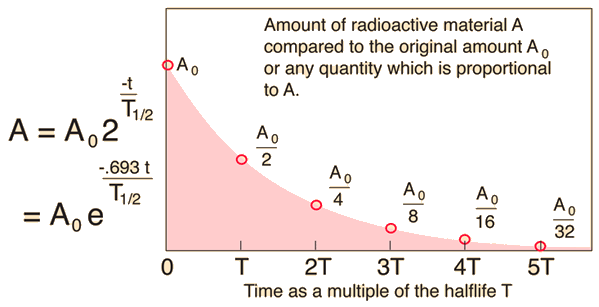
enter image source here

The original mass is #m_0=12.0g#

After #19# days, amount remaining is #m_19=0.375g#

The ratio of #m_19/m_0=0.375/12=1/32#

That is

#m_0/m_19=32#

#m_19=1/32m_0#

The half life is #=t_(1/2)#

#m_19# corresponds to #5t_(1/2)#

So,

#5t_(1/2)=19#

#t_(1/2)=19/5=3.8# days

We can perform the calculation

#m_19=m_0e^(-19lambda)#

#e^(-19lambda)=m_19/m_0=1/32#

#19lambda=ln(32)#

#lambda=1/19ln(32)=5/19ln2#

#t_(1/2)=ln2/lambda=ln2/(5/19ln2)=19/5=3.8#days