What is the equation of the parabola with a focus at (-2, 6) and a vertex at (-2, 9)?
3 Answers
y - 9 = 1/12 ( x + 2 )^2
Explanation:
Generic Equation is
y - k = 1/4p ( x - h)^2
p is distance vertex to focus = 3
(h,k) = vertex location = (-2, 9)
Explanation:
When talking about the focus and vertex of a parabola, the easiest way to write the equation is in vertex form. Luckily, you already have most of your information.
However, we do not have the value of
We know this because the only difference between the two coordinates is the
Now that you have your value for
y=-x^2/12-x/3+26/3
Explanation:
Given -
Vertex
Focus
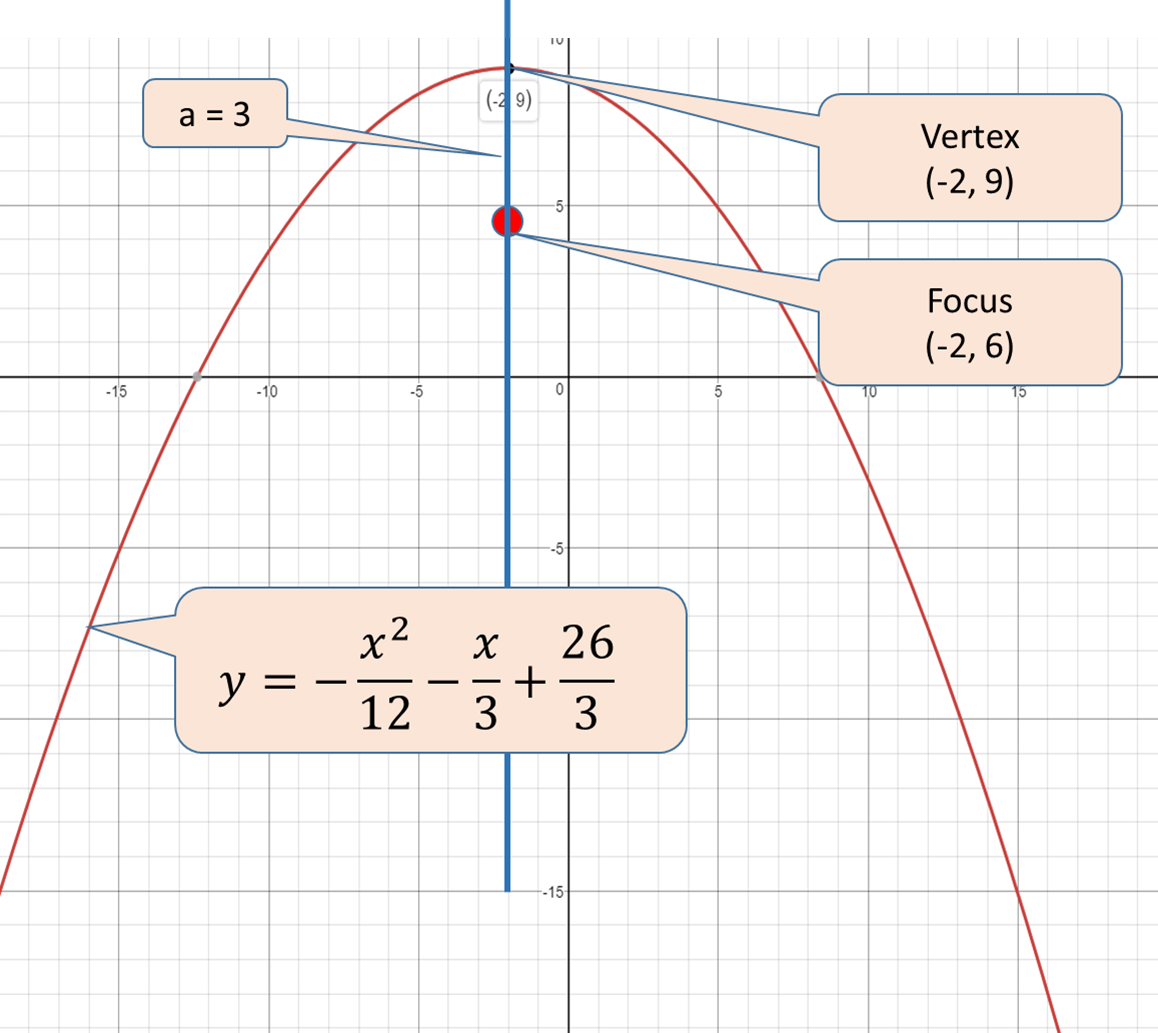
The focus of the parabola lies below the vertex. Hence, it opens down.
The formula for downward opening parabola having origin as its vertex is -
x^2=-4ay
The vertex of the given parabola is not at the vertex. it is in the 2nd quarter.
The formula is -
(x-h)^2=-4xxaxx(y-k)
h=-2 x-coordinate of the vertex
k=9 y-coordinate of the vertex
a=3 Distance between vertex and focus
Substitute the values in the formula
(x+2)^2=-4xx3xx(y-9)
x^2+4x+4=-12y+108
-12y+108=x^2+4x+4
-12y=x^2+4x+4-108
y=-x^2/12-4/12x+108/12
y=-x^2/12-x/3+26/3



