How to calculate the potential energy of an electron in the #"nth"# shell (also take example #"n=3"# shell) of a copper atom using the Hartree Fock Theory? Also calculate its kinetic energy
1 Answer
You can't calculate the kinetic energy of an electron that hasn't left the atom. So we could only calculate the orbital potential energy.
DISCLAIMER: COMPLICATED ANSWER!
Since copper is not that heavy, we don't have to worry too much about scalar relativistic effects or spin-orbit coupling. In fact, its ground electronic state is a
The ground-state electron configuration would be:
#[Ar] 3d^10 4s^1#
INPUT FILE SETUP
At the Hartree-Fock level of theory (a single-reference method), we assume a single configuration with doubly-occupied core and
MolPro, Psi4, and other computational software could do this, but I have MolPro with me right now. A basic input for copper atom would look like this:
[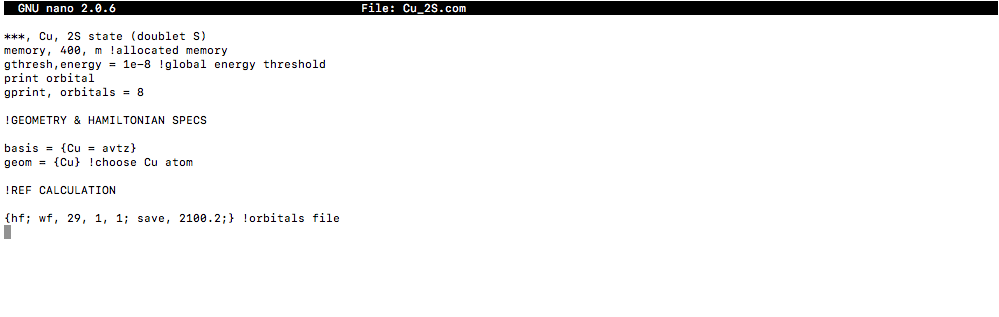
Here,
#400# megawords are used for the memory (32 bits per word on a 32-bit machine, etc).- Only the Abelian point groups are used, and by default for atoms,
#bb(D_(2h))# is used. - copper is using an augmented correlation-consistent polarized valence triple zeta basis set, with basic atomic geometry specified.
- The atom has
#29# electrons, the unpaired electron is of#A_g# symmetry (symmetry 1), and has twice the total spin,#2 xx S# , of#1# , as specified by the wave function card:
#"wf, 29, 1, 1"#
VERIFYING THE ORBITAL OCCUPATION
The orbitals in the basis set are being printed in order by energy within each irreducible representation of the
So, orbital
We expect the orbital occupation is ordered as follows:
#ul(A_g" "B_(3u)" "B_(2u)" "B_(1g)" "B_(1u)" "B_(2g)" "B_(3g)" "A_u)#
#1s" "2p_x" "2p_y" "3d_(xy)" "2p_z" "3d_(xz)" "3d_(yz)" "-#
#2s" "3p_x" "3p_y" "" "" "color(white)(.)3p_z#
#3s" "#
#3d_z^2" "#
#3d_(x^2 - y^2)#
#color(red)(4s)" "# where red indicates the singly-occupied orbital with one spin-up electron.
MolPro believes it to be:
[
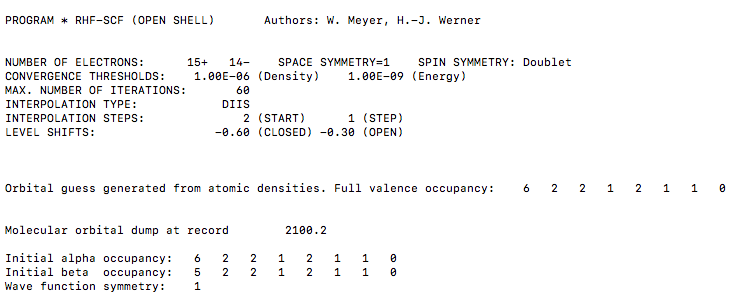
The orbital occupation looks correct on the first go, but in practice, you should specify the occ and closed cards anyway. It should be an occupied configuration of:
#(A_g, B_(3u), B_(2u), B_(1g), B_(1u), B_(2g), B_(3g), A_u) = (6, 2, 2, 1, 2, 1, 1, 0)# , specified by
#"occ, 6, 2, 2, 1, 2, 1, 1, 0"# within the brackets for the HF command.and a closed-shell (doubly-occupied) configuration of:
#(A_g, B_(3u), B_(2u), B_(1g), B_(1u), B_(2g), B_(3g), A_u) = (5, 2, 2, 1, 2, 1, 1, 0)# , specified by
#"closed, 5, 2, 2, 1, 2, 1, 1, 0"# within the brackets for the HF command
indicating one spin-up electron in the
ORBITAL ENERGIES (BE CRITICAL!)
The orbital output was:
[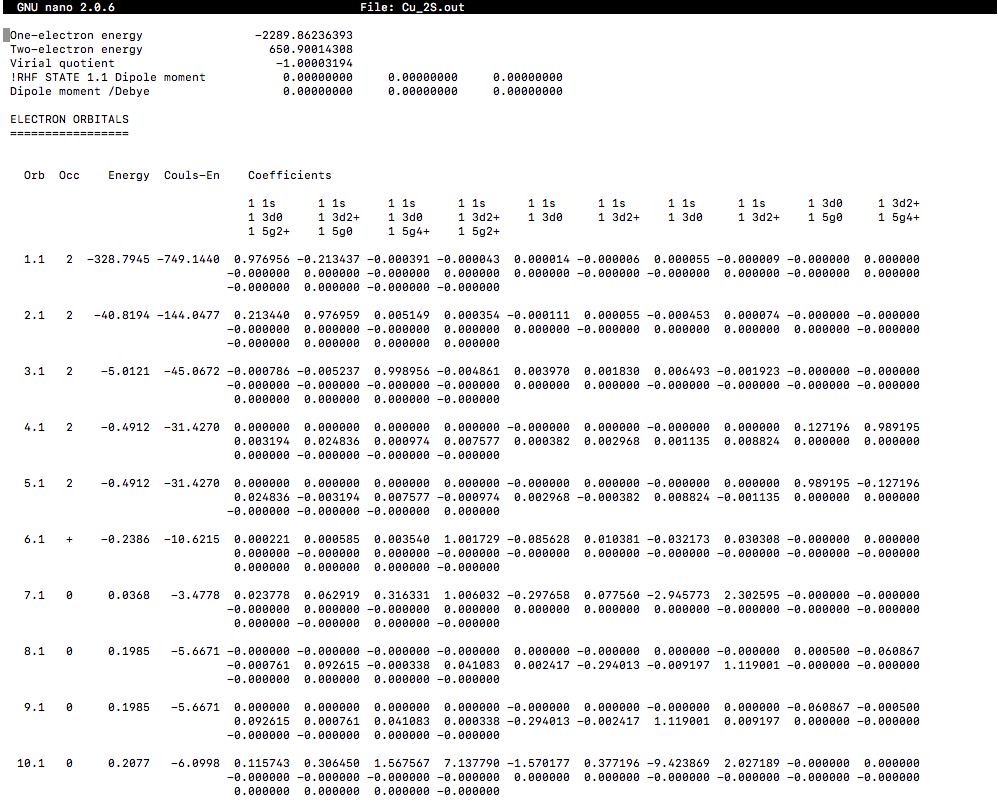
The default energies listed are in Hartrees, so you'll have to convert to
Apparently, the HOMO, the
The
The
For a basic calculation at a low level of theory, this isn't that bad...

