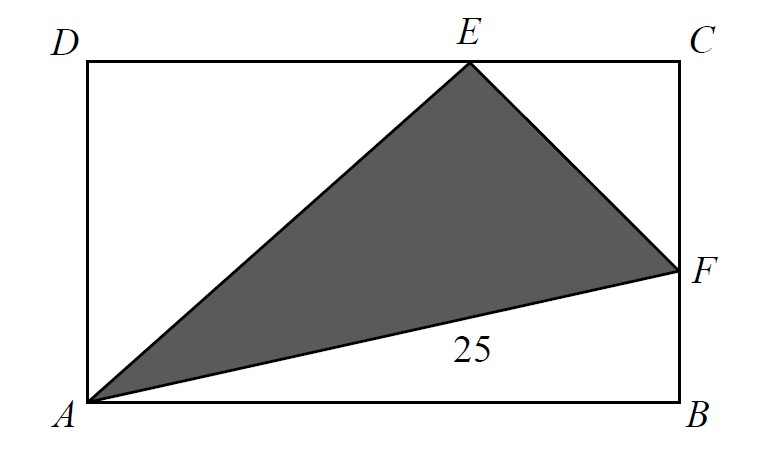
ABCD is a rectangle with E as a point on CD and F is a point on BC such that #angle#AEF = #90^@# and AF = 25cm. The length of DE, EC, CF, FB, AE and EF are positive integers. What is the area of rectangle ABCD, in cm2?
1 Answer
Explanation:
Let's start by finding
#AE^2 + EF^2 = 25^2#
One possibility is the
The only other right triangles we can make are ones where everything is scaled up by a certain factor. In this case, 25 only has factors of 5, so the only other triangles we can make are ones with a hypotenuse of
The only Pythagorean triple with a hypotenuse of
#5# is the#3# -#4# -#5# triangle.If we multiply all of the sides of this triangle by
#5# , we get that the legs must be#3*5=15# and#4*5=20# . Since the diagram depicts#AE# as being longer than#EF# , let's say that:
#AE = 20#
#EF = 15#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now we've figured out our two leg lengths for the shaded triangle. As it turns out, these two legs are both a hypotenuse for another triangle which must have all integer side lengths. Let's start with the triangle with
#AD^2 + DE^2 = 20^2#
Using trial and error, or from memory, one can deduce that the only pair of numbers which produce a hypotenuse of 20 is (yet again) a
This time, we need to scale everything up by a factor of
#4# . This means that our#3# -#4# -#5# triangle turns into a#12# -#16# -#20# triangle.
This means that the two legs of this triangle are
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The same thing can be done for the triangle with hypotenuse
Again, we see that we must take a
#3# -#4# -#5# triangle and scale it up. This time, it is by a factor of 3.This means our
#3# -#4# -#5# triangle becomes a#9# -#12# -#15# triangle.
This means that the two legs of this triangle are
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We have one final triangle to solve -- the one with
The only other Pythagorean triple with
This means that the two legs of this triangle are
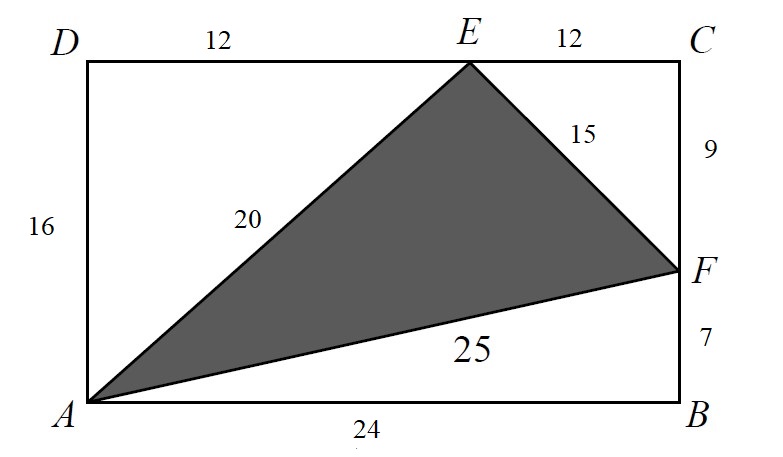
The dimensions in the figure now appeaar as shown below:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now, to find the area of the whole rectangle. Notice that we've found the leg lengths of all 4 triangles that this shape was divided into. This means that we can find the areas of all 4 triangles, and then simply add them all together to get the area of the rectangle.
#A = 1/2(15)(20) + 1/2(12)(16) + 1/2(9)(12) + 1/2(7)(24)#
#A = 150 + 96 + 54 + 84#
#A = 384# or just#16xx24=384#
So the area of the rectangle is
Final Answer

