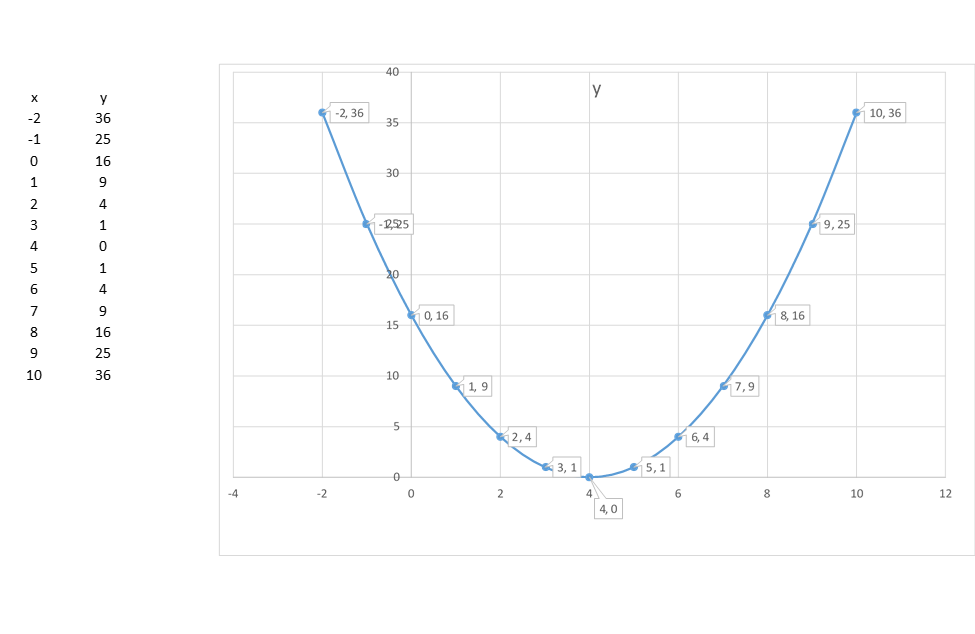
How do you graph the parabola #Y=(x-4)^2# using vertex, intercepts and additional points?

Question

2170 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-03T00:36:02

Y-intercept #(0, 16)

x-intercept #(4,0)#

Vertex #(4,0)#

Given -

#y=(x-4)^2#

It's y- intercept at #x=0#

#y=(0-4)^2=(-4)^2=16#
#(0, 16)#

Its x - intercept at #y=0#

#(x-4)^2=0#
#x-4=0#
#x=4#

At #x=4 ; y=(4-4)^2=0#

#(4,0)#

Vertex

Find the minimum point

#dy/dx=2(x-4)xx1#
#dy/dx=2x-8#
#dy/dx =0 => 2x-8=0#
#x=8/2=4#
X- coordinate of the vertex #x=4#

Its y-coordinate of the vertex is #y=(4-4)^2=0#
Vertex #(4,0)#

Vertex is the same as minimum point

For graph

enter image source here