Question

A box with an initial speed of `2 m/s` is moving up a ramp. The ramp has a kinetic friction coefficient of `3/2` and an incline of `(2 pi )/3`. How far along the ramp will the box go?

Answer 1

`"distance" = 0.126` `"m"`

Explanation:

We're asked to find how far the box will travel up the ramp, given its initial speed, the coefficient of kinetic friction, and the angle of inclination.

I will solve this problem using only Newton's laws and kinematics (i.e. without using work/energy).

NOTE: Ideally, the angle of inclination would be between `0` and `pi/2`, so I'll choose the corresponding first-quadrant angle of `pi/3`.

I will also take the positive `x`-direction as *up the ramp.*

When the box reaches its maximum distance, the instantaneous velocity will be `0`. We are ultimately going to use the constant-acceleration equation

`ul((v_x)^2 = (v_(0x))^2 + 2a_x(Deltax)`

where

• `v_x` is the instantaneous velocity (which is `0`)

• `v_(0x)` is the initial velocity

• `a_x` is the (constant) acceleration

• `Deltax` is the distance it travels (what we're trying to find)

Since the velocity `v_x = 0`, we can also write this equation as

`0 = (v_(0x))^2 + 2a_x(Deltax)`

We also figure that the acceleration will be negative because it slows down and comes to a brief stop at its maximum height, so we then have

`0 = (v_(0x))^2 + 2(-a_x)(Deltax)`

And we can move it to the other side:

`ul(2a_x(Deltax) = (v_(0x))^2`

Rearranging for the distance traveled `Deltax`:

`ulbar(|stackrel(" ")(" "Deltax = ((v_(0x))^2)/(2a_x)" ")|)`

We already know the initial velocity, so we need to find the acceleration of the box.

`" "`

Let's use Newton's second law of motion to find the acceleration, which is

`ul(sumF_x = ma_x`

where

• `sumF_x` is the net force acting on the box

• `m` is the mass of the box

• `a_x` is the acceleration of the box (what we're trying to find)

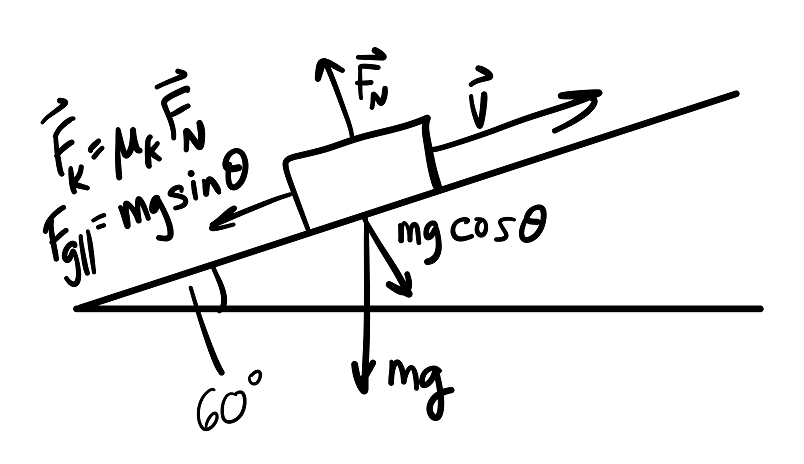
The only forces acting on the box are

• the gravitational force (acting down the ramp), equal to `mgsintheta`

• the friction force (acting down the ramp), equal to `mu_kn`

And so we have our net force equation:

`sumF_x = mgsintheta + mu_kn`

The normal force `n` exerted by the incline is equal to

`n = color(purple)(mgcostheta)`

So we can plug this in to the net force equation above:

`ul(sumF_x = mgsintheta + mu_kcolor(purple)(mgcostheta)`

Or

`ul(sumF_x = mg(sintheta + mu_kcostheta)`

Now, we can plug this in for `sumF_x` in the Newton's second law equation:

`sumF_x = ma_x`

`ma_x = mg(sintheta + mu_kcostheta)`

We can cancel the mass `m` by dividing both sides by `m`, leaving us with

`color(green)(ul(a_x = g(sintheta + mu_kcostheta)`

`" "`

Now that we have found an expression for the acceleration, let's plug it into the equation

`Deltax = ((v_(0x))^2)/(2a_x)`

And we get

`color(red)(ulbar(|stackrel(" ")(" "Deltax = ((v_(0x))^2)/(2g(sintheta + mu_kcostheta))" ")|)`

We're given in the problem

• `v_(0x) = 2` `"m/s"`

• `theta = (pi)/3`

• `mu_k = 3/2`

• and the gravitational acceleration `g = 9.81` `"m/s"`

Plugging these in:

`color(blue)(Deltax) = ((2color(white)(l)"m/s")^2)/(2(9.81color(white)(l)"m/s"^2)(sin[(pi)/3] + 3/2cos[(pi)/3])) = color(blue)(ulbar(|stackrel(" ")(" "0.126color(white)(l)"m"" ")|)`

Answer 2

Here's my own attempt at this problem, using an alternative approach to Nathan's, to see if our answers agree. Like Nathan, I will assume that you mean to have the ramp right-side-up, i.e. an angle of `60^@` w.r.t. the horizontal...

I also got `"0.126 m"`.

---

My approach here is via conservation of energy:

`DeltaE = DeltaK + DeltaU + W_(vecF_k) = 0`

where:

• My coordinate axes are almost the usual vertical `y` and horizontal `x`. Rightwards is `+x`, but downwards is `+y`.
• `DeltaK = 1/2 mv_f^2 - 1/2 mv_i^2 = m/2(v_f^2 - v_i^2)`
• `DeltaU = mvecgDeltavecy = mgy_f`, where `y_i = 0`, `y_f < 0`, and `g > 0`. The potential energy becomes more negative due to the sign of `y_f`.
• `W_(vecF_k) = vecF_kd` is the counteracting work due to kinetic friction (negative w.r.t. the box, the system). In this case, I define

`d = sqrt((Deltax)^2 + (Deltay)^2) - 0 = sqrt(x_f^2 + y_f^2)` with `x_i = 0` and `x_f > 0`. `d` is then the final position, `< 0`.

Currently, we know we have a nonzero initial velocity and a zero final velocity when the box comes to a stop:

`=> DeltaK = -m/2v_i^2`

This so far gives:

`-m/2v_i^2 + mgy_f + vecF_kd = 0`

or

`m/2v_i^2 - mgy_f - vecF_kd = 0`

Using the sum of the forces:

`sum_i vecF_(_|_,i) = vecF_N - mvecgcostheta = 0`

So...

`0 = cancel(m)/2v_i^2 - cancel(m)gy_f - mu_kcancel(m)vecgcosthetad`

`=> 1/2 v_i^2 - gy_f - mu_kgcosthetad = 0`

Now, we can rewrite `y_f` in terms of `d`, the distance traveled along the ramp:

`y_f = dsintheta < 0`

This gives:

`=> 1/2 v_i^2 - gdsintheta - mu_kgdcostheta = 0`

Solve for `d` to get:

`d = (1/2 v_i^2)/(gsintheta + mu_kgcostheta)`

`= (v_i^2)/(2g(sintheta + mu_kcostheta))`

(which is also what Nathan found, by the way.)

So, in the end, we get:

`color(blue)(|d|) = (2^2)/(2(9.81)(sin(60^@) + 3/2cos(60^@)))`

`=` `color(blue)("0.126 m")`