Question

How do you convert `y=-y^2+3x^2-xy` into a polar equation?

Answer 1

`r = (2sintheta)/(6cos^2theta-2sin^2theta -sin2theta)`

Explanation:

In order to convert between Cartesian and polar equations, we must make use of the following three identities:

`x -=rcostheta`

`y -= r sintheta`

`x^2+y^2 -= r^2`

`y= -y^2+3x^2-xy`

`rsintheta = -r^2sin^2theta +3r^2cos^2theta-r^2sinthetacostheta`

`sintheta = r(-sin^2theta+3cos^2theta -sinthetacostheta)`

`r = (2sintheta)/(6cos^2theta-2sin^2theta -sin2theta)`

Answer 2

Use the formulas `x = rcos(theta) and y = rsin(theta)`
Use algebraic methods to write the radius `r` as a function of `theta`

Explanation:

Before we begin, let's take a look at the graph of the Cartesian equation:

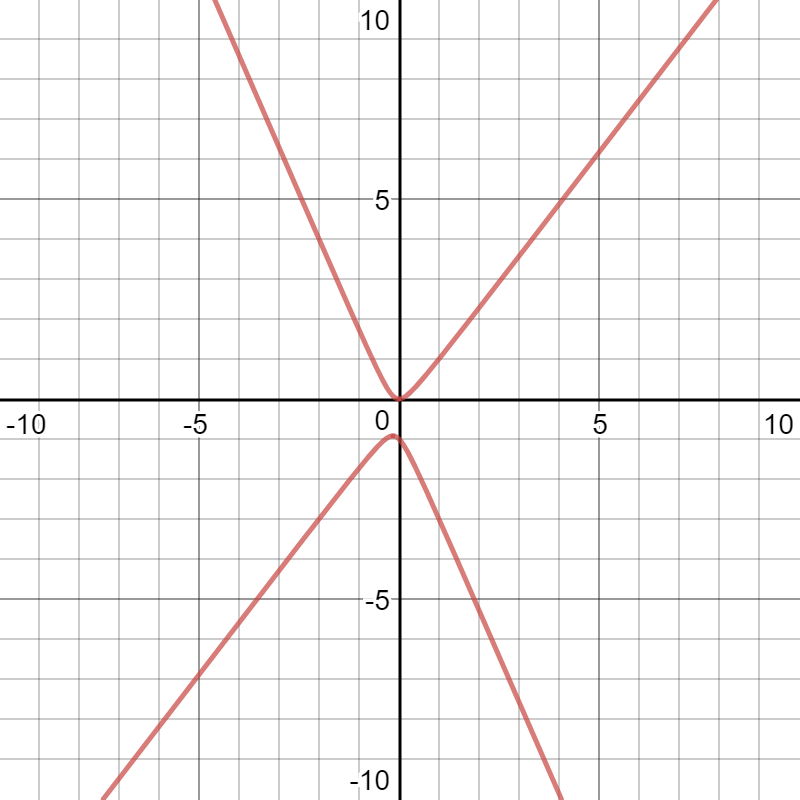
Substitute `rcos(theta)` for every x and `rsin(theta)` for every y:

`rsin(theta) = -(rsin(theta))^2+3(rcos(theta))^2 - (rcos(theta))(rsin(theta)`

Remove the common factor, `r^2`, from the right:

`rsin(theta) = r^2(-sin^2(theta)+3cos^2(theta) - cos(theta)sin(theta))`

We can divide both sides by r, because that only discards the degenerative root `r=0` and the graph will still contain that point when `theta = 0`:

`sin(theta) = r(-sin^2(theta)+3cos^2(theta) - cos(theta)sin(theta))`

Divide both sides by the coefficient of r:

`r= sin(theta)/(-sin^2(theta)+3cos^2(theta) - cos(theta)sin(theta))`

The following is a graph of the polar equation:

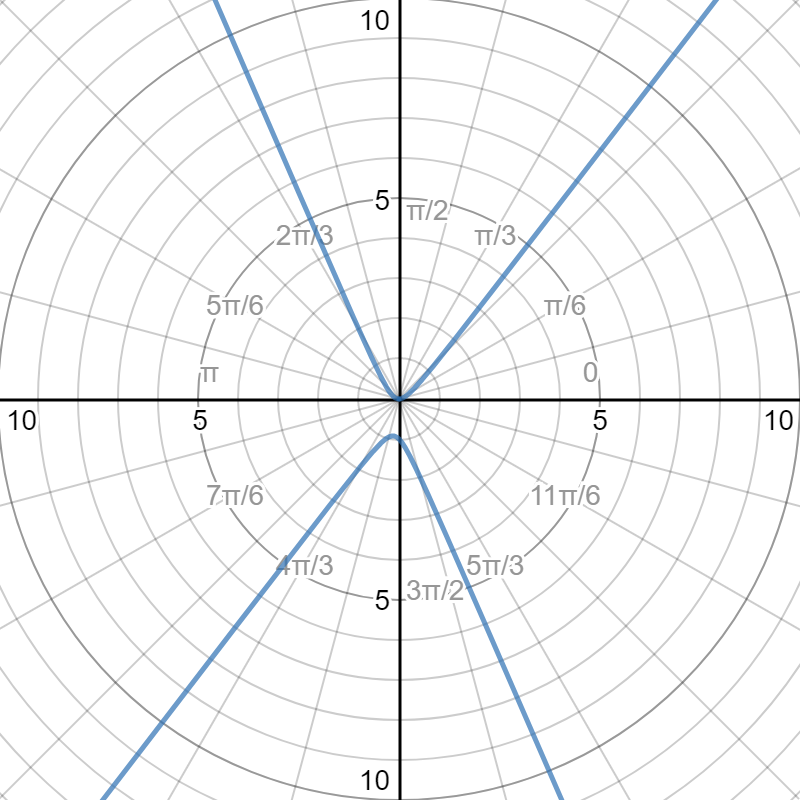
Please observe that the graphs are identical.