Question

An object with a mass of `12 kg` is lying still on a surface and is compressing a horizontal spring by `1/3 m`. If the spring's constant is `6 (kg)/s^2`, what is the minimum value of the surface's coefficient of static friction?

Answer 1

`mu_s<=0.017`

Explanation:

We can use Newton's second law to solve.

Diagram:

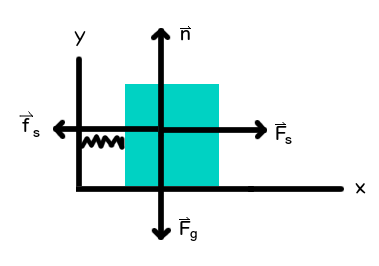
We have the following information:

• `|->m=12" kg"`
• `|->Deltas=-1//3" m"`
• `|->k=6" kg"//"s"^2`
• `|->g=9.81"m"//"s"^2`

`=>`Note that the displacement is negative for a compressed spring as the final position is more negative than the initial position.

We can sum the forces parallel and perpendicular:

`sumF_x=F_s-f_s=0`

`sumF_y=n-F_g=0`

• Note that the net force in both directions is 0 as the object remains at rest. The system is in a state of static equilibrium.

We also know:

• `f_(s"max")=mu_sn=>f_s<=mu_sn`

• `F_s=-kDeltas`

• `F_g=mg`

Substituting the above equations into the statements we formed above:

• `n=mg`

• `-kDeltas-mu_(s"max ")mg=0`

We can solve for `mu_(s"max")`:

`color(darkblue)(mu_(s"max ")=(-kDeltas)/(mg))`

Submitting in our known values:

`mu_(s"max ")=-((6" kg"//"s"^2)(-1//3" m"))/((12" kg")(9.81"m"//"s"^2)`

`=>~~0.017`

Therefore, `color(darkblue)(mu_s<=0.017)`.