Why does more heat transfer take place in a reversible process than in a irreversible process?
Well, here we have defined dS = δQrev/T....
and the second law of thermodynamics (Clausius inequality) says dS ≥ δQ/T (Here δQ is just the differential of heat regardless of it being reversible or irreversible) Here the equality holds for it being a reversible process (as defined)...
so: dS ≥ δQ/T
If I put dS on the left as δQrev/T,
I will get δQrev/T ≥ δQ/T
or δQrev ≥ δQ
This implies that in a reversible process, more heat transfer takes place than in an irreversible one....why is this so?
Well, here we have defined dS = δQrev/T....
and the second law of thermodynamics (Clausius inequality) says dS ≥ δQ/T (Here δQ is just the differential of heat regardless of it being reversible or irreversible) Here the equality holds for it being a reversible process (as defined)...
so: dS ≥ δQ/T
If I put dS on the left as δQrev/T,
I will get δQrev/T ≥ δQ/T
or δQrev ≥ δQ
This implies that in a reversible process, more heat transfer takes place than in an irreversible one....why is this so?
1 Answer
Another variation on this answer is given here.
REVERSIBLE PROCESSES
A reversible process is one that is done infinitesimally slowly. It can be thought of as the most efficient possible way to carry out a certain thermodynamic event, i.e. a reversible heat flow wastes no thermal energy. There is no such process in real life, but we can get close.
As you know, we can write using the second law of thermodynamics:
#dS = (deltaq_"rev")/T# where:
#d# is an exact differential and#delta# is inexact. The former corresponds to a state function, and the latter to a path function.A state function does not depend on the path taken, but a path function does.
#S# is the entropy (a measure of energy dispersal) and#q# is the heat flow.#"rev"# denotes the reversible process.
Since entropy is a state function, the change in entropy must be representable as a closed integral such that:
#ointcolor(white)(1)dS = oint (deltaq_"rev")/T = 0#
This is saying that if a process starts in one spot and ends up in the same spot, no matter what path taken, the change in entropy must be zero.
It follows that the process must have perfectly reversed itself in the second half of its path, leading to zero entropy change!
Now, with a nontrivial path where
#DeltaS = int_((1))^((2)) 1/T deltaq_"rev"#
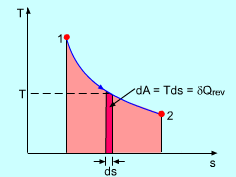
You can see that there are no gaps (no missed areas under the curve).
IRREVERSIBLE PROCESSES
An irreversible process, however, has lost some energy along the way. For instance, one can transfer heat, wait a moment, and then continue again.
The moment of pause allows heat to transfer into another system in such a way that it is difficult to take it through the microscopic reverse and gain it back.
A common way to represent this is through a step-ladder process:
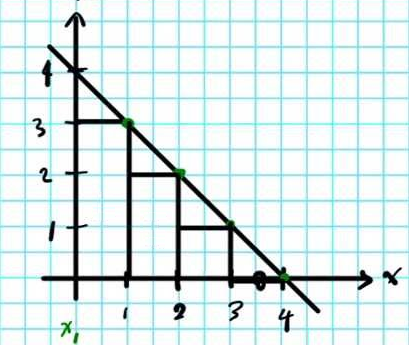
It's like approximating (and underestimating) the area under the curve for the
#DeltaS > 1/T(q_1 + q_2 + q_3)# where
#q_"rev" > q_1 + q_2 + q_3# .
The reason why
#ointdS ne 0# if#dS = (deltaq_"irr")/T# .
Lastly, note that another way to write the above equation is that
#q_"rev" = q_"irr" + q_"lost"#
or
#[DeltaS_"rev" = q_"rev"/T] = q_"irr"/T + q_"lost"/T#
When we generalize this, since
#color(blue)(DeltaS >= q/T)# ,
or for infinitesimal changes,
#color(blue)(dS >= (deltaq)/T)# .where the
#># applies to#q_"irr"# and#=# applies to#q_"rev"# .

