Find all the #8^(th)# roots of #3i-3#?
Find all the #8^(th)# roots of
#3i-3#
Also show any one of them in an Argand diagram.
Find all the
Also show any one of them in an Argand diagram.
1 Answer
Explanation:
Let
First, we will put the complex number into polar form:
# |omega| = sqrt((-3)^2+3^2) =3sqrt(2)#
# theta =arctan(3/(-3)) = arctan(-1) = -pi/4#
# => arg \ omega = pi/2+pi/4 = (3pi)/4 #
So then in polar form we have:
# omega = 3sqrt(2)(cos((3pi)/4) + isin((3pi)/4)) #
We now want to solve the equation
# z^8 = 3sqrt(2)(cos((3pi)/4) + isin((3pi)/4)) #
Whenever dealing with complex variable equation such as this it is essential to remember that the complex exponential (and therefore the polar representation) has a period of
# z^8 = 3sqrt(2)(cos((3pi)/4+2npi) + isin((3pi)/4+2npi)) \ \ \ n in ZZ #
By De Moivre's Theorem we can write this as:
# z = 3sqrt(2)(cos((3pi)/4+2npi) + isin((3pi)/4+2npi))^(1/8) #
# \ \ = (3sqrt(2))^(1/8)(cos((3pi)/4+2npi) + isin((3pi)/4+2npi))^(1/8) #
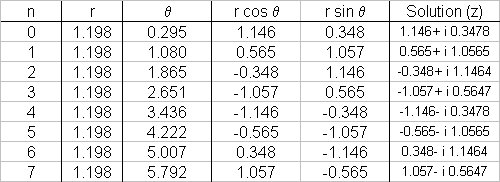
# \ \ = 3^(1/8)2^(1/16) (cos(((3pi)/4+2npi)/8) + isin(((3pi)/4+2npi)/8))#
# \ \ = 3^(1/8)2^(1/16) (cos theta + isin theta ) #
Where:
# theta =((3pi)/4+2npi)/8 = ((3+8n)pi)/32#
And we will get

After which the pattern continues (due the above mentioned periodicity).
We can plot these solutions on the Argand Diagram:


