Question #b1cd1
1 Answer
Because gases really aren't always negligible in size compared to their container, particularly at high pressures and low temperatures.
Using
#barV_"real" = "2.1508 L/mol"# (Actual value)
#barV_"RK" = "2.1827 L/mol"# (Redlich-Kwong,#1.48%# error)
#barV_"vdW" = "2.2324 L/mol"# (van der Waals,#3.79%# error)
#barV_"id" = "2.3904 L/mol"# (Ideal Gas Law,#11.1%# error!!)
And it is clear that the ideal gas law overestimates the size of
Under these conditions, according to its phase diagram:
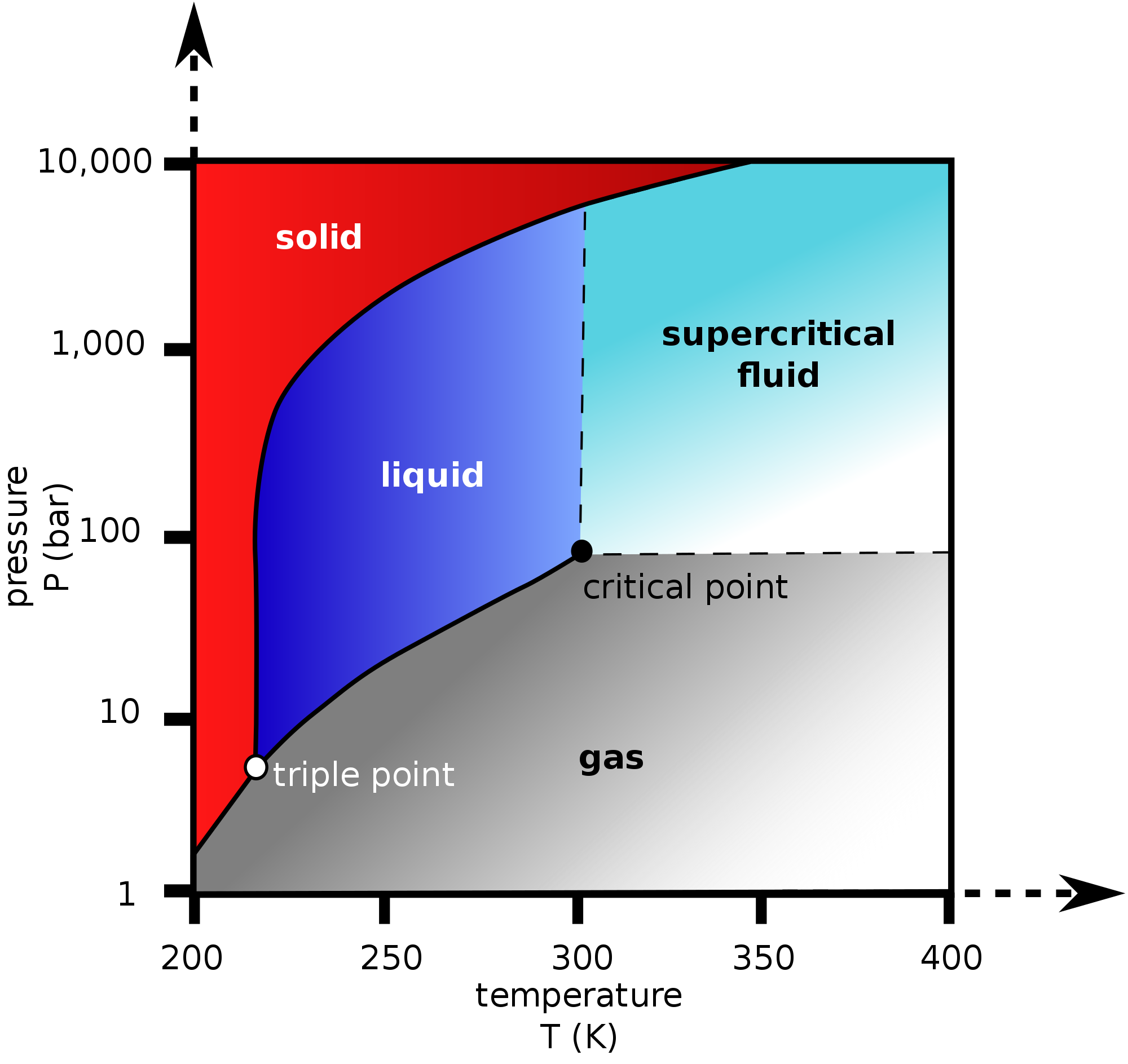
...
VAN DER WAALS EQUATION OF STATE
The van der Waals (vdW) equation of state is given by:
#P = (RT)/(barV - b) - a/(barV^2)# where:
#P# ,#V# ,#n# ,#R# , and#T# are known from the ideal gas law.#barV = V/n# is the molar volume.#a# is a vdW constant that accounts for the attractive and repulsive forces in the gas sample. Its units can be#"L"^2cdot"bar/mol"^2# if pressure is in#"bar"# .#b# is a vdW constant that accounts for the volume excluded by the gas particles (#b > 0# ). Its units are#"L/mol"# .
This equation gives better agreement than the ideal gas law would, particularly at higher pressure and lower temperatures where the ideal gas law fails.
EXAMPLE: CO2
Consider
#color(green)(barV_"real") = "1 L"/(20.4617 cancel"g") xx (44.009 cancel"g")/"mol" = ulcolor(green)("2.1508 L/mol")#
The ideal gas law would give:
#color(green)(barV_"id") -= V/n = (RT)/P#
#= (("0.083145 L"cdotcancel"bar""/mol"cdotcancel"K")(230 cancel"K"))/cancel"8 bar"#
#=# #ulcolor(green)("2.3904 L/mol")# which is fairly off, though it isn't bad. It means we used the equation in a physically valid situation.
With the vdW equation, however, we may get a better result. For
One would solve for
#PbarV^3 - (bP + RT)barV^2 + abarV - ab = 0#
In an iterative calculation (Newton-Raphson method), one could solve this equation to get three roots. Choosing the correct root would yield:
#color(blue)(barV_"vdW" = ul"2.2324 L/mol")#
It's not perfect, but it is definitely closer than the ideal gas law was.
Alternatively, the more complicated Redlich-Kwong equation of state, with
#barV_"real" = "2.1508 L/mol"#
#barV_"RK" = "2.1827 L/mol"#
#barV_"vdW" = "2.2324 L/mol"#
#barV_"id" = "2.3904 L/mol"#
This illustrates the lack of ideality that a gas could exhibit at high pressure and low temperature.

