What is the equation of the parabola with a focus at (-3,1) and a directrix of y= -1?
1 Answer
Sep 11, 2017
#y=x^2/4+(3x)/2+9/4#
Explanation:
Given -
Focus
Directrix
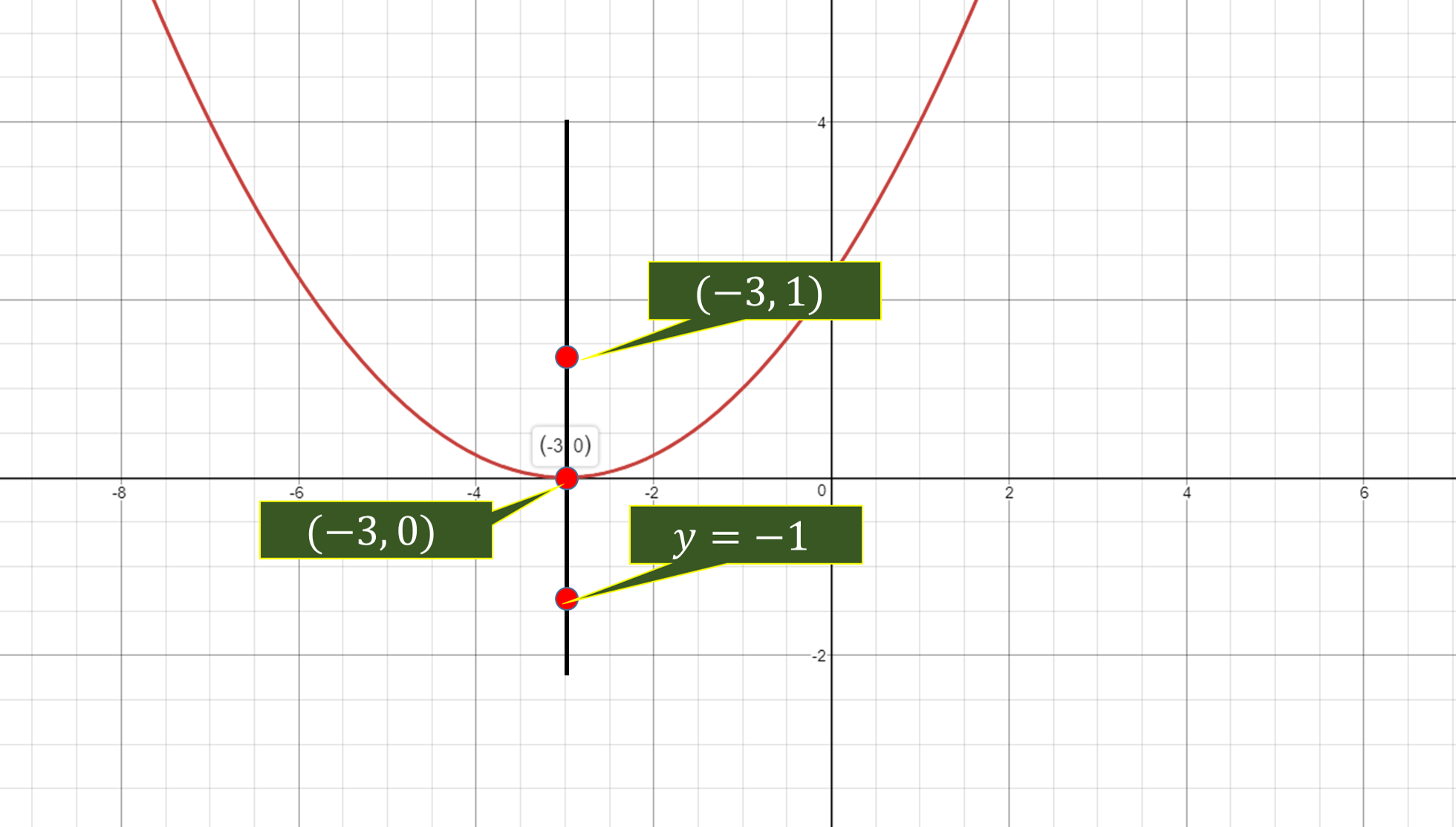
From the given information, we understand the parabola is opening up.
The vertex lies in between Focus and directrix at the middle.
The vertex is
Then the vertex form of the equation is
#(x-h)^2=4xxaxx(y-k)#
Where -
#h= -3#
#k=0#
#a=1# The distance between focus and vertex or directrix and vertex.
#(x-(-3))^2=4 xx 1 xx( y-0)#
#(x+3)^2=4y#
#4y= x^2+6x+9#
#y=x^2/4+(3x)/2+9/4#

